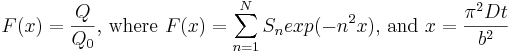Other Links:
-
Helium Evidence for A Young
World Remains Crystal-Clear
-
D. Russell Humphreys replies to Henke.
Dr. Humphreys' reply raises even more questions about the quality and
accuracy of his work, including his ability to distinguish an intrusive
igneous rock (biotite granodiorite) from a partially veined strongly
foliated (metamorphic) gneiss. The chemistry of the light and dark layers
of this gneiss do not even resemble a granodiorite. By sampling zircons from
multiple lithologies, Dr. Humphreys has undermined the veracity of his
creationist "model."
Rather than emphasizing a pretty diagram (Figure 2 in this reply) that can
provide dates from hundreds to millions of years, Dr. Humphreys needs to
properly address the truthfully chaotic results of his creationist "model,"
which are listed in Dr. Henke's Tables 5 and
6. Additionally, if extraneous
3He and
4He
are detected in the Fenton Hill zircons, the contamination event
could easily generate the "6,000 year old" curve in Dr. Humphreys' Figure 2.
Underestimating the uranium content of the zircons is another factor that
can negatively impact Dr. Humphreys' claims. Until Dr. Humphreys properly
deals with all of these issues, he cannot expect his work to be taken
seriously in authentic peer-reviewed geology journals.
Dr. Henke is also disappointed that Dr. Humphreys' questions the sincerity
of his former religious beliefs. Before speculating on Dr. Henke's past
beliefs and motives, Dr. Humphreys should have read Dr. Henke's
autobiographical writings. Dr. Humphreys' reply and additional errors will
be addressed in detail in the upcoming months.
Humphreys' reply is also availiable in a
PDF version. This box was added on May 3, 2005.
|
ABSTRACT
For decades, young-Earth creationists (YECs) have
desperately sought "scientific evidence" to attack
radiometric dating and protect their religious
interpretations of Earth history. In 2003, many Christian
fundamentalists became very excited about YEC statements in
Humphreys et al.
(2003a), Humphreys et
al. (2003b) and Humphreys
(2003). Humphreys et
al. (2003a) claim that zircons from the "Jemez
Granodiorite" (Fenton Hill rock core, New Mexico, USA)
contain too much "radiogenic" helium to be billions of
years old. By "modeling" the helium diffusion rates in the
zircons and assuming some unfounded miraculous increases in
radioactive decay rates, Humphreys et al. (
2003b, 2004) concluded that the zircons are only "6,000
± 2,000 years old." Not surprisingly, their results
conveniently straddle Bishop Ussher's classical 4004 BC
"Genesis creation date" for the world.
The results in Humphreys
et al. (2003a) and related YEC documents are
clearly based on numerous invalid assumptions, flawed
arguments, and questionable data, which include:
- invoking groundless miracles to explain away U/Pb dates
on zircons,
- misidentifying samples as originating from the Jemez
Granodiorite,
- performing helium analyses on impure biotite
separations,
- dubiously revising helium measurements from Gentry et al.
(1982a),
- relying on questionable Q/Q0 (helium
retention) values from Gentry
et al. (1982a),
- failing to recognize that the Q0
values (maximum possible amount of radiogenic helium in a
mineral) for their samples were probably much greater than
15 ncc STP/μg,
- inconsistently interpreting already questionable helium
concentrations from samples 5 and 6 to make them comply
with the demands of their "models,"
- seriously underestimating the helium concentrations in
the zircons from 750 meters depth and not realizing that
their Q/Q0 value for this sample (using
Q0 = 15 ncc STP/μg) would be greater
than one and therefore spurious,
- not properly considering the possible presence of
extraneous ("excess") 3He and 4He in
their zircons,
- listing the average date and standard deviation of
their 2004 results as 6,000 ±2,000 years when a
standard deviation (two-sigma) of ± 4,600 years is
more appropriate.
- "fudging" old Soviet data that should have been
ignored,
- deriving "models" that are based on several invalid
assumptions (including constant temperature conditions over
time, Q0 of 15 ncc STP/μg, and
isotropic diffusion in biotite),
- failing to provide standard deviations for biotite
measurements (b values) and then misapplying the
values to samples from different lithologies,
- inserting imaginary defect lines into Arrhenius plots,
and
- deriving and using equations that yield inconsistent
"dates."
The relatively high Q/Q0 values of
some of the Fenton Hill core zircons may be due to
extraneous helium or artifacts of grossly underestimating
the Q0 values of uranium- and
thorium-rich zircons. Because of these and other problems,
the YEC "dates" and conclusions in
Humphreys et al.
(2003a) and related documents are completely
unreliable.
INTRODUCTION
Because radiometric dating methods conflict with their
biblical interpretations, young-Earth creationists (YECs)
desperately want to undermine the reliability of these
methods. Although YECs claim to believe that the
Bible is the
"powerful word of God", they fully realize that just
quoting their scriptures is not going to convince
geochronologists and other scientists to abandon their
research and stream to church altars in repentance.
Therefore, a small group of YEC Ph.D.s associated with the
Institute for Creation
"Research" (ICR), the Creation "Research"
Society (CRS) and formerly "Answers" in
Genesis (AiG) formed the
RATE (Radioisotopes and the Age of
The Earth) committee (Vardiman et al., 2000;
Humphreys et al.,
2004, p. 3). Simply put, their activities include
combing the scientific literature and designing laboratory
"experiments" that will somehow verify what they have
already concluded, namely that a "literal" interpretation
of Genesis is "The Truth" and anything
that conflicts with their biblical interpretations is
"wrong."
In late 2003, ICR,
AiG, YEC computer scientist Dr.
David A. Plaisted, YEC Barry
Setterfield,
Apologetics Press, and many other YEC groups and
individuals became very excited by a series of claims in
Humphreys et al. (2003a) (Adobe Acrobat [pdf]
file) (html version is
here and also here).
Updated information on this RATE project is summarized in
Humphreys et al. (2003b) (Adobe Acrobat file),
Humphreys
(2003), and
Humphreys et al. (2004).
Many YECs sincerely believe that these articles are
excellent examples of high quality "research" by YEC
"scientists" and a crowning achievement for the RATE
committee.
The discussions in Humphreys et al.
(2003a) and related documents primarily deal with the
diffusion of helium from uranium- and thorium-bearing zircons
(zirconium silicate, ZrSiO4). Helium includes
two major isotopes: 3He and 4He.
3He, which only has one neutron per atom, is
"primordial" (Dalrymple, 1984,
p. 112); that is, the isotope is a product of the Big Bang
(Delsemme, 1998, p. 22-23) and
nuclear fusion in stars (Faure,
1998, p. 17). Some 3He was trapped within
the Earth when our planet formed. 3He is
currently degassing from the Earth's interior.
4He, which has two neutrons in every atom, is
another product of the Big Bang and stellar fusion (Delsemme, 1998, p. 22-23; Faure, 1998, p. 17). Additionally,
4He (alpha particles) may form from the
radioactive decay of uranium and thorium. The following
information from Langmuir
(1996, p. 490-491) and
Gentry et al. (1982a, p. 1129) (Adobe Acrobat
file) lists the half-lives (T1/2) of
238U, 235U and 232Th, the
resulting stable lead daughters, and the total number of
4He atoms produced from the decay of each
uranium or thorium isotope to their stable leads:
238U → 206Pb + 8
4He with T1/2 = 4.51 x 109
years
235U → 207Pb + 7
4He with T1/2 = 7.1 x 108
years
232Th → 208Pb + 6
4He (a branching ratio) with T1/2 =
1.41 x 1010 years
Using analogous definitions for argon in McDougall and Harrison
(1999, p. 11), helium may be classified as "radiogenic"
or "extraneous." Radiogenic helium refers to 4He
that forms from the radioactive decay of uranium and
thorium in a mineral (such as a zircon) and then remains
trapped within the mineral. In contrast, 3He and
ex-situ 4He are extraneous helium. That
is, if 4He escapes from its source mineral and
enters and contaminates surrounding fluids or rocks, it
becomes extraneous. Volcanism and tectonic activity may
cause both 3He and 4He to rise from
the Earth's interior, mix, accumulate in minerals in the
upper crust, and then perhaps eventually escape into the
atmosphere (also see Baxter,
2003).
Humphreys et al.
(2003a,b; 2004) and Humphreys
(2003) discuss the supposed "young Earth" implications
of their helium diffusion experiments with zircons. The
zircons were taken from Precambrian subsurface samples
collected in 1974 from the Fenton Hill GT-2/EE-2 borehole
site (Humphreys, 2003;
Gentry et al., 1982b, p. 296 [Adobe Acrobat
file]) about 56 kilometers west of Los Alamos, New Mexico,
USA. Humphreys et al.
(2003a, p. 3 [the page numbers for this document are
based on the Adobe Acrobat (pdf) format])
admit that uranium-lead (U/Pb) dates indicate that
their zircons contain about 1.5 billion years worth of
radiogenic lead. At the same time, they argue that the tiny
zircons contain too much "radiogenic" helium to be billions
of years old. That is, these YECs believe that the helium
should have escaped from the zircons long ago if they
really are 1.5 billion years old. By studying helium
diffusion rates, Humphreys
et al. (2003a) initially concluded that the
zircons must only be 4,000 to 14,000 years old.
Subsequently in Humphreys
et al. (2003b; 2004) and Humphreys (2003), the "age" of
the zircons was further restricted to 6,000 ± 2,000
years (one sigma standard deviation using the "biased"
equation [i.e., n and not n-1 in the
denominator; Davis, 1986, p. 33;
Keppel, 1991, p. 43-44, 58]; see
discussions below). Not surprisingly, their new "age range"
conveniently straddles Bishop
Ussher's classical 4004 BC "Genesis creation date" for
the world.
YECS MISUNDERSTAND SCIENCE
To avoid any accusations of heresy from other YECs,
Humphreys et al. must "reconcile" their helium
diffusion results with their 1.5 billion year old U/Pb
dates in a manner that only favors their religious agenda.
To explain away the U/Pb dates, Humphreys et al.
(2003a; 2004, p. 11) use a reprehensible YEC
tactic that authentic scientists would never consider -
they invoke a miracle. Humphreys et al.
(2003a, p. 7; 2004, p. 11) claim that God created a
"brief burst of accelerated nuclear decay," which
supposedly produced the necessary amounts of radiogenic
lead and helium in a short period of time without melting
and sterilizing the Earth. Specifically, Humphreys et al.
(2003a, p. 7) state:
"As before, the creation model starts with a brief burst
of accelerated nuclear decay generating a high
concentration C0 of helium uniformly throughout
the zircon (like the distribution of U and Th atoms), but
not in the surrounding biotite."
Humphreys et al.
(2004, p. 11) further reiterate:
"Thus our new diffusion data support the main hypothesis
of the RATE research initiative: that God drastically
accelerated the decay rates of long half-life nuclei during
the earth's recent past."
Humphreys et al.
(2003a, p. 15) further speculate that their global
"burst of accelerated nuclear decay" could have occurred
during the "Creation Week," "the Fall of Adam and Eve,"
and/or "Noah's Flood." However, for some reason, Humphreys
et al. never explain why the Crucifixion of Jesus
Christ was not important enough to warrant one of these
supposed "accelerated decay events." No matter which Bible
stories are invoked to explain their unsubstantiated
"accelerated radioactive decay events," Humphreys et
al. must then conjure up additional miraculous excuses
to keep the heat of these "events" from vaporizing Adam
and/or frying Noah and crew.
Because Humphreys et al. are happy with their
supposed "helium diffusion age" of 6000 ± 2000
years, they have no need to extend the miracles to affect
the diffusion rates of radiogenic helium through zircons
and biotites. Indeed, Humphreys et al.
(2004, p. 11) readily admit that they don't want to
deal with the life-threatening problems that would result
from God universally accelerating diffusion rates:
"But diffusion rates are tied straightforwardly to the
laws of atomic physics, which are in turn intimately
connected to the biochemical processes that sustain life.
It is difficult to imagine any such drastic difference in
atomic physics that would have allowed life on earth to
exist."
The nice thing about unproven and imaginary miracles is
that individuals can readily turn them on and off to
achieve whatever results they want!
Of course, an "accelerated nuclear decay event" is
nothing more than an example of the infamous Gosse
(Omphalos) fallacy (also
here) and has absolutely no place in science or
reality. Anyone can use their imaginations to invoke a
miracle to "explain away" any problem they don't like.
Because YECs are often willing to "resolve" any problems or
prop up any of their religious ideas with unfalsifiable
ad hoc
miracles, they really don't produce scientific results or
models. In contrast, scientists work to rationally solve
problems rather than making them vanish with a "Bible
wand." Clearly, if Humphreys et al. or anyone else
want to reject natural processes and invoke magic to
protect their religious, political or philosophical
doctrines from rebuttal, then they have the responsibility
of presenting definitive evidence of a miracle. As
explained below, the discussions in Humphreys et al.
(2003a) and related YEC documents don't even come close
to justifying the need for a miracle.
Rather than defending the absurdities of their Gosse
actions, Humphreys et
al. (2003a, p. 4) play an old YEC game and blame
scientists for supposedly being biased, narrow-minded and
dogmatic because they only embrace the "uniformitarian
assumption of invariant decay rates." However, what else
can scientists do, especially when the evidence indicates that
decay rates have been constant over time? (For example, see
McDougall and Harrison,
1999, p. 10, for discussions on the uniformity of the
40K decay rate.) How can the
scientific method function if anyone is allowed to
conjure up miracles to explain away any problem or scenario
that they don't like? While YECs often denounce the
methodological naturalism of the scientific method
because it excludes magic from scientific hypotheses, YECs
forget that methodological naturalism is the foundation of
criminal forensics, modern medicine and every
other scientific discipline. If psychologists
don't blame demons for causing manic depression, forensics
scientists don't invoke witchcraft to solve unwitnessed
crimes, and defense lawyers don't claim that Voodoo curses
were responsible for an unwitnessed murder, why should
geologists use the supernatural to explain the origin of a
rock?
REACTIONS TO HUMPHREYS ET AL.'S
YEC CLAIMS
Not surprisingly, YEC reactions to the claims in Humphreys et al.
(2003a) and related YEC documents have been
overwhelmingly positive and too often carelessly
uncritical. Like many YECs,
Carl Wieland of AiG is very confident and proud of the
RATE results. He
suggests that "uniformitarians" (that is,
actualists or scientists) are in an inescapable trap
because of the supposed thoroughness of Humphrey et
al.'s work:
"The [Humphreys et al., 2003a] paper looks at the
various avenues a long-ager might take by which to wriggle
out of these powerful implications, but there seems to be
little hope for them unless they can show that the
techniques used to obtain the results were seriously (and
mysteriously, having been performed by a world-class
non-creationist expert [Dr. Kenneth A. Farley])
flawed."
As stated in Humphreys
et al. (2003a, p. 20), geochemist Dr. Kenneth A.
Farley (anonymously referred to as the "experimenter"
in Humphreys et al.,
2004) performed the helium diffusion analyses for this
RATE project. Nevertheless, Dr. Wieland clearly
misunderstands how scientists view the work of other
scientists. Although Dr. Farley is a well-respected expert,
scientists don't consider him or any other colleague to be
an infallible pope or prophet. Again, in contrast to
Wieland's misconceptions of science and the scientific
method, scientists don't appreciate YECs that invoke
groundless and unproven
miracles to "resolve" any "contradictions" between U/Pb
ages and helium diffusion results. If there are any
contradictions in geochronology, geochronologists would
patiently and persistently look for natural explanations
just as other scientists do when solving crimes or
diagnosing illnesses.
The analytical procedures and results in Humphreys et al.
(2003a) and related YEC documents have been extensively
criticized by a number of individuals, including: Dr. Joseph G.
Meert and especially an anonymous reviewer
"WeHappyFew," whose comments are linked at "More
Second-Rate Science by the RATE Group" by Jack DeBaun.
Humphreys
has replied to some of Meert's criticisms. More recently,
Humphreys et al.
(2004, p. 9, 12-15) respond to criticisms by
old-Universe creationist Ross
(2003) and the comments of an anonymous critic.
Unfortunately, Humphreys et
al. (2004) don't have the courtesy and courage to
identify the critic or even reference his/her document(s).
Unless privacy issues are involved, authors should identify
their opponents and the opponents' literature so that
readers can readily evaluate both sides of an issue and
fairly make up their own minds.
Despite some inaccurate
statements by RATE critics, a careful review of Humphreys et al.
(2003a,b; 2004), Humphreys
(2003), their key references, claims from Humphrey
et al.'s YEC allies, and comments by various
skeptics of RATE demonstrate that Humphreys et al.'s
"research" is based on unsubstantiated claims, questionable
numbers, invalid assumptions, inconsistent equations, and
many flawed arguments. As discussed below, some of their
mistakes may be trivial. However, other errors and
uncertainties completely undermine any confidence in
Humphreys et al.'s claims.
IMPROPER SAMPLE IDENTIFICATION AND
HANDLING TECHNIQUES
Humphreys et al. Misidentify their
Rock Samples
When performing research, scientists must carefully
follow all quality control/quality assurance (QC/QA)
procedures. Essential QC/QA procedures include properly
collecting, identifying, labeling, storing and monitoring
all samples. If the collection site of a specimen is
unknown or if it has been improperly stored for several
decades, any resulting data are often useless.
Unfortunately for them, Humphreys and his colleagues
have failed to comply with the most fundamental QC/QA
requirements. Throughout their article (2003a), Humphreys
et al. claim that they have studied biotites and
zircons from samples of the "Jemez Granodiorite" collected
at a depth of 750 meters from the Fenton Hill borehole
site. While Gentry et al.
(1982a) properly recognized that some of the Fenton
Hill borehole samples are gneisses, Humphreys et al.
(2003a, p. 3) erroneously assert that all six
subsurface samples in Gentry
et al. (1982a) came from this granodiorite. More
recently, Humphreys et
al. (2004, p. 5; 2003b) continue to refer to their
"granodiorite" samples from depths of 750 and 1490 meters.
Nevertheless, a review of the subsurface geology of the
Fenton Hill borehole site as described in Sasada (1989, Figure 2, p. 258 - NOT
"Sakada" as listed in the references of Humphreys et
al., 2003a, p. 16 and Humphreys et al., 2004, p.
16) indicates that a granodiorite is not encountered at the
site until depths of more than 2500 meters. According to Sasada (1989, p. 258), Precambrian
gneisses and mafic schists occur between depths of 722
meters and to slightly below 2500 meters. In particular, at
depths of 750 and 1490 meters, Humphreys et al.
(2003a,b) clearly sampled a Precambrian gneiss (a
highly metamorphosed volcanic, intrusive or sedimentary
rock) and not a granodiorite (an intermediate intrusive
igneous rock) (Table 1).
Table 1: Information on the Fenton Hill, New
Mexico, well core from Gentry
et al. (1982a, p. 1130) and Humphreys et al.
(2003a,b), including helium concentrations (Q in
nano cubic centimeters of helium per microgram of zircon at
standard temperature and pressure [STP], ncc STP/μg)
from Gentry et al.
(1982a, p. 1130), revised helium (Q) values in
Humphreys et al.
(2003a, p. 3), and original data from Humphreys et al.
(2004). The geology is from Sasada (1989, p. 258). Surface
temperatures and depths are from Humphreys et al.
(2004, Table I, p. 3). The ratios of measured helium to
theoretical radiogenic helium (Q/Q0
values, defined in text below) are from Humphreys et al.
(2003a,b; 2004).
| Sample No. |
Depth (meters) |
Subsurface Temp. °C |
Lithology |
Gentry et al.'s He measurements
(Q)
(ncc STP/μg) |
Revised He measurements in Humphreys et al.
(Q) (ncc STP/μg) |
Q/Q0 ±30% |
| 0 |
0 |
20 |
Bandelier Tuff |
82 |
8.2 |
----- |
| 2002 |
750 |
96 |
Precambrian Gneiss |
---- |
~12.1 |
~0.80 |
| 1 |
960 |
105 |
Precambrian Gneiss |
86 |
8.6 |
0.58 |
| 2003 |
1490 |
124 |
Precambrian Gneiss |
----- |
6.3 |
0.42 |
| 2 |
2170 |
151 |
Precambrian Gneiss and/or Mafic Schist |
36 |
3.6 |
0.27 |
| 3 |
2900 |
197 |
Jemez Granodiorite |
28 |
2.8 |
0.17 |
| 4 |
3502 |
239 |
Jemez Granodiorite? |
0.76 |
0.16 |
0.012 |
| 5 |
3930 |
277 |
Jemez Granodiorite? |
~0.2 |
~0.02 |
~0.001 |
| 6 |
4310 |
313 |
Jemez Granodiorite? |
~0.2 |
~0.02 |
~0.001 |
YECs might argue that because Precambrian granodiorites
and gneisses were all magically zapped into existence
during the six 24-hour days of the "Creation Week"
(e.g.,
Snelling and Woodmorappe, 1998, p. 530),
distinctions between Precambrian rocks really aren't
important. Despite the fact that YECs invoke myths and
miracles to explain away most Precambrian intrusive rocks
(e.g.,
Snelling and Woodmorappe, 1998, p. 530), Humphreys et al.
(2003a, p. 2) unintentionally admit that at least some
intrusive rocks have significant histories when they claim
that zircon crystals become imbedded in larger crystals as
a magma "cools and solidifies." Nevertheless, in contrast
to YEC fantasies about rocks magically forming during a
"Creation Week," scientists recognize that gneisses and
granodiorites have very different and often complex
origins, chemistries, and histories. This is especially
true for gneisses, which (by definition) have undergone one
or more high-temperature metamorphic heating events after
the formation of their precursor igneous or sedimentary
rocks (Hyndman, 1985, p. 442).
Of course, like an old scratched phonograph record or a
dented old car (scroll down),
the properties of a metamorphosed rock often indicate a
long and complex history.
Besides lithological and chemical dissimilarities, the
ages of the Jemez Granodiorite and the overlying gneiss
that Humphreys et al.
(2003a,b; 2004) actually studied are noticeably
different. Zartman (1979)
provides a date of 1500 ± 20 million years old for
the biotite granodiorite (Jemez) at a depth of 2,903.8
meters. Not surprisingly, the zircons from the Precambrian
gneiss at 750 meters depth provide a somewhat younger date
of 1439.3 ± 1.8 million years old (Appendix A of
Humphreys et al., 2003a).
Zartman (1979, p. 18) also
found that the U/Pb dates for the zircons and epidotes from
the Jemez granodiorite were discordant. The U/Pb results in
the table of Appendix A of Humphreys et al.
(2003a, p. 17) also indicate discordant conditions for
the gneiss. U/Pb discordance is due to the loss of lead and
intermediate daughters (in most cases) and/or uranium
addition (Faure, 1998, p.
289-290), probably because of metamorphism or other
alteration events. The origin of gneissic textures in the
rocks studied by Humphreys et al. would require one
or more metamorphic events and these events could have
caused lead losses (Faure, 1998,
p. 288-290). Because helium atoms are uncharged, smaller
and therefore much more mobile than lead, any events that
resulted in lead loss probably would have caused much
greater losses of radiogenic helium.
YECs might argue that misidentifying a gneiss as the
Jemez Granodiorite is not a serious mistake and that this
error would not significantly affect their zircon diffusion
studies or their "dating" results. However, this
misidentification is more serious than YECs might realize.
As discussed below, Humphreys et al. have
unknowingly taken laboratory measurements from a gneiss and
then misapplied them to dating samples 3-5, which are from
the Jemez Granodiorite and perhaps deeper lithologies. In
the following statements, Humphreys et al.
(2003a, p. 6) even admit that mixing experimental
results from different rock types is not appropriate:
"Measurements of noble gas diffusion in a given type of
naturally occurring mineral often show significant
differences from site to site, caused by variations in
composition. For that reason it is IMPORTANT to get helium
diffusion data on zircon and biotite from the SAME rock
unit (the Jemez Granodiorite) which was the source of
Gentry’s samples." [my emphasis]
This sample misidentification blunder also says a lot
about Humphreys et al.'s inability to pay careful
attention to important geological details and it raises
some serious doubts about the quality and reliability of
their other work.
Inadequate Biotite Separations from the
750-Meter Sample
Successful helium diffusion studies on biotites and
zircons require mineral samples that are sufficiently pure.
In Appendix C of Humphreys
et al. (2003a, p. 20), Dr. Kenneth A. Farley
notes that the purity of the 750-meter zircon samples was
good:
"We verified that the separate was of high purity and
was indeed zircon."
In contrast, the following statements by Dr. Farley and
Humphreys et al. {in braces} in Appendix B of
Humphreys et al. (2003a, p. 19) raise serious doubts
about the acceptable purity of the 750-meter biotites:
"He diffusion in this [Fenton Hill core biotite] sample
follows a rather strange pattern, with a noticeable curve
at intermediate temperatures. I have no obvious explanation
for this phenomenon. Because biotite BT-1B [Beartooth
Gneiss, Wyoming, USA] did not show this curve, I doubt it
is vacuum breakdown. I ran more steps, with a drop in
temperature after the 500°C step, to see if the
phenomenon is reversible. It appears to be, i.e.,
the curve appears again after the highest T step,
but the two steps (12, 13) that define this curve had very
low gas yield and high uncertainties. It is possible that
we are dealing with more than one He source (multiple grain
sizes or multiple minerals?). {We [Humphreys et al.]
think it is likely there were some very small
helium-bearing zircons still embedded in the biotite
flakes, which would be one source. The other source would
be the helium diffused out of larger zircons no longer
attached to the flakes.}"
According to Humphreys
et al. (2004), Jakov Kapusta of Activation
Laboratories, Ltd., extracted the biotites and zircons from
both the 750-meter (p. 4-5) and 1490-meter (p. 5) samples.
However, Humphreys et
al. (2003a, p. 6, 17) give a different account and
claim that ICR personnel were responsible for extracting
the biotites from the 750-meter specimen. Considering the
ICR's
poor record at separating specific minerals from rocks,
it's not surprising that Farley and Humphreys et al.
(2003a) would discover impurities in the biotites if ICR
personnel were actually responsible for the separations. Of
course, separating minerals from rocks is not easy and pure
separations are not always possible. Nevertheless, many
geochemical studies require high purity separations even if
it means sorting and cleaning microscopic grains by hand.
Because Humphreys et
al. (2003a, p. 19) admit that their samples
probably contain microscopic zircon impurities or other
sources of helium contamination, the 750-meter biotite
results in their Appendix B cannot be trusted.
MYSTERIOUS CHANGES IN GENTRY et
al.'S DATA
In 1982, YEC Robert V. Gentry was lead author on a
couple of peer-reviewed articles on the zircons of the
Fenton Hill GT-2/EE-2 cores. Table 1 in Humphreys et al.
(2003a, p. 3) borrows a lot of information from the
table in Gentry et al.
(1982a, p. 1130). In a footnote with their reference 9
(Gentry, "Glish" [sic, Gush] and McBay; i.e.,
Gentry et al., 1982a), Humphreys et al.
(2003a, p. 15) comment on several changes that were
made to the Gentry et al.
(1982a) data when they were imported into Humphreys et al.
(2003a, p. 3):
"After consulting with Dr. Gentry, I [Humphreys?] have
corrected, in the third column of my Table 1, two apparent
typographical errors in the corresponding column of his
table. One is in the units of the column, the other is in
sample 4 of that column. The crucial ratios
Q/Q0 in column four were correctly
reported, as we have confirmed with our own data."
A similar statement is made in Humphreys et al.
(2004, p. 16).
My Table 1 summarizes the differences between the
original data in Gentry et
al. (1982a, p. 1130) and the revisions in Humphreys et al.
(2003a, p. 3). For example, the helium concentration of
sample 4 was modified from 0.76 to 0.16 nano cubic
centimeters (standard pressure and temperature, STP)
He/microgram zircon (ncc STP/μg; Table 1). Humphreys
et al. in consultation with Gentry also reduced the
concentrations of the other helium measurements by ten
times. Although Gentry et
al. (1982a) contains several obvious typographic
errors (for example, the depth of the lowermost core sample
is sometimes listed as "11310" instead of 4310 meters), the
changes involving the helium results are suspicious and
could be more likely a response to innocent math or
measurement errors than simply correcting miscopied numbers
from a laboratory notebook. Clearly, Humphreys et al.
(2003a) should have provided more details to justify
these mysterious changes. To thwart any unfair and cynical
accusations of data manipulation, they should also explain
how the mistakes in Gentry et
al. (1982a) were discovered and why these errors
went unnoticed for more than 20 years.
QUESTIONABLE Q/Q0
VALUES
A Q/Q0 value compares the measured and expected helium
values for a zircon or other mineral.
Q refers to the
measured quantity of helium (presumably
only radiogenic 4He) in a mineral. From its
crystallization to the present, Q0 is the
maximum amount of radiogenic helium
(4He) that could accumulate in a mineral from
the radioactive decay of its uranium and thorium (Humphreys et al.,
2003a, p. 3). Q0 assumes no diffusion
loss ("leakage") of helium from the host mineral over time
or any helium contamination from outside sources
(i.e., extraneous helium). To estimate the
theoretical maximum amounts of radiogenic helium in their
zircons (Q0), Gentry et al. (1982a, p.
1129) made several questionable assumptions:
"For the other zircons from the granite [sic,
granodiorite] and gneiss cores [samples 1-6], we made the
assumption that the radiogenic Pb concentration in zircons
from all depths was, on the average, the same as that
measured (Zartman, 1979) at 2900
m, i.e., ~80 ppm with
206Pb/207Pb and
206Pb/208Pb ratios of ten (Gentry
et al., ...[1982b]; Zartman,
1979). Since every U and Th derived atom of
206Pb, 207Pb, and 208Pb
represents 8, 7 and 6 alpha-decays respectively, this means
there should be ~7.7 atoms of He generated for every Pb
atom in these zircons."
Although Q0 assumes "negligible
diffusion loss" of helium over time, Gentry et al. (1982a, p.
1129) applied "compensation factors" to their calculations
because they recognized that radiogenic helium could
initially escape from a zircon grain if
the decay occurred close to the edge of the grain or within
a very small zircon. The escape of helium from a zircon
during its radiogenic formation is called "alpha ejection"
(Farley et al., 1996;
Tagami et al., 2003).
Once a 4He (alpha) particle forms from
radioactive decay, the particle will typically travel about
11 to 29 microns in a zircon grain before stopping (Farley et al., 1996, p.
4224). Gentry et al.
(1982a, p. 1129-1130) assume that 30-40% of the
radiogenic helium in their small (40-50 microns) zircons
was lost because of "alpha ejection." Equations in Tagami et al. (2003, p.
59) indicate that helium loss through alpha ejection is
probably closer to 50% for zircons with lengths and widths
of about 40-50 microns and perhaps a 40% loss for the 50-75
micron zircons in Table 1 of Gentry et al. (1982a).
Nevertheless, Gentry et
al. (1982a) do not adequately explain how the
"compensation factors" were exactly used in their
calculations. They simply (p. 1130) state:
"The uncertainties in our estimates of the zircon masses
and compensation factors probably mean these last
[Q/Q0] values are good to only
±30%."
Humphreys et al.
(2004, p. 9) state that Gentry obtained an overall
Q0 value of about 15 ncc STP/μg for
the zircons in samples 1-6. Adequate details on how this
value was derived are not in Gentry et al. (1982a),
Gentry et al. (1982b)
or any of the Humphreys documents.
Using available information from Gentry et al. (1982a),
the revised helium measurements in Humphreys et al.
(2003a, p. 3) and ignoring the possibility of
extraneous 4He and 3He, I was unable
to derive a Q0 of 15 ncc STP/μg for
the zircons. Instead, I calculated Q0 as
41 ncc STP/μg. Therefore, my Q/Q0
values for samples 1-6 are different. My detailed
calculations of Q0
and Q/Q0 are shown in Appendix A at the end of this
document. In Table 2, my Q/Q0 values are
compared with the values from Gentry et al. (1982a)
and Humphreys et al.
(2003a).
Table 2: Estimated Q/Q0 values
for zircons in the Fenton Hill well cores using assumptions
from Gentry et al.
(1982a, p. 1130) and revised data from Humphreys et al.
(2003a, p. 3; 2004) (also, see my Table 1). My detailed
calculations are in Appendix
A.
| No. |
Depth (m) |
He measurements in Humphreys et al. (Q)
(ncc STP/μg) |
Gentry et al.'s and Humphreys et al.'s
Q/Q0 (Q0 = 15 ncc
STP/μg) |
My calculated Q/Q0
(Q0 = 41 ncc STP/μg) |
| 1 |
960 |
8.6 |
0.58 |
0.21 |
| 2 |
2170 |
3.6 |
0.27 |
0.088 |
| 3 |
2900 |
2.8 |
0.17 |
0.068 |
| 4 |
3502 |
0.16 |
0.012 |
0.0039 |
| 5 |
3930 |
~0.02 |
~0.001 |
~0.0005 |
| 6 |
4310 |
~0.02 |
~0.001 |
~0.0005 |
Considering the questionable assumptions and vague
explanations in Gentry et
al. (1982a) and Humphreys et al.
(2003a; 2004), their methods for calculating
Q/Q0 values are probably erroneous.
Unfortunately, statistically reliable Q and
Q0 values are not available for
individual zircons from samples 1-6. Therefore, a less
definitive approach must be used to test the plausibility
of the Q/Q0 values in Gentry et al. (1982a)
and Humphreys et al.
(2003a,b; 2004). Using uranium and thorium data on
individual zircon grains from Gentry et al. (1982b)
and a number of unavoidable assumptions, I derived an
alternative set of Q/Q0 values for the
zircon grains from samples 1, 5, and 6 (Table 3). The
detailed calculations are shown in Appendix B.
Table 3: My revised Q/Q0 values
derived from uranium and thorium data on zircons from
samples 1, 5 and 6 (Gentry et
al., 1982b). My detailed calculations are shown in
Appendix B.
| Zircon ID |
Depth (m) |
Uranium (parts per million) in zircons |
Thorium (parts per million) in zircons |
Q/Q0 in Humphreys et al.
(2003a) |
Maximum and Minimum Q/Q0 values
using Q values from Humphreys et al.
(2003a) |
| |
|
|
|
|
|
| 1A |
960 |
240 - 5300 |
800 - 2000 |
0.58 |
0.011 - 0.21 |
| 1B |
960 |
465 - 1130 |
220 - 750 |
0.58 |
0.047 - 0.17 |
| 1C |
960 |
1250 -3300 |
100 - 275 |
0.58 |
0.018 - 0.067 |
| 5A |
3930 |
83 - 220 |
63 - 120 |
~0.001 |
~0.0005 - 0.002 |
| 5B |
3930 |
90 - 110 |
60 - 90 |
~0.001 |
~0.001 - 0.002 |
| 6A |
4310 |
110 - 550 |
40 - 85 |
~0.001 |
~0.0002 - 0.002 |
| 6B |
4310 |
125 - 210 |
63 -175 |
~0.001 |
~0.0006 - 0.001 |
The Q/Q0 values in Gentry et al. (1982a),
Humphreys et al.
(2003a,b; 2004), and my Tables 2 and 3 are certainly
far from ideal. However, I would argue that my values in
Tables 2 and 3 are the best that we can currently obtain.
Although my Q/Q0 zircon results at depths
of 3930 and 4310 meters (samples 5 and 6 in Table 1) are
similar to those in Humphreys
et al. (2003a) and Gentry et al. (1982a),
my values from 960 meters (sample 1) and samples 2-4 in
Table 2 are always significantly lower. The calculations in
Appendix B also clearly indicate
that Q0 values may be substantially
greater than the 15 ncc STP/μg proposed by Gentry et al. (1982a)
and Humphreys et al.
(2004, p. 9). Because (as discussed below)
Q0 and the resulting
Q/Q0 values have important roles in the
helium diffusion "models" and "dates" of Humphreys et al.
(2003a, equations 12, 14a-b, 16, etc.) and associated
RATE documents, lower values would significantly erode
their YEC interpretations and claims.
HIGHER THAN EXPECTED HELIUM
CONCENTRATIONS IN ZIRCONS FROM DEPTHS OF 750 METERS
As stated in Humphreys
et al. (2003a, p. 20), Dr. Farley performed
helium analyses on zircons from a depth of 750 meters in
the Fenton Hill GT-2 borehole core. Again, these zircons
were taken from a gneiss and not the Jemez Granodiorite as
Humphreys et al.
(2003a) repeatedly claim. During the study, non-YEC Dr.
Farley was not informed that he was providing data for a
YEC project (Humphreys et
al., 2003a, p. 6-7).
In Appendix C of Humphreys
et al. (2003a, p. 20), Dr. Farley refers to the
zircon samples (750-meters depth) as releasing "540"
nanomoles of helium/gram of sample (nmol/g) (or ~12.1 x
10-9 cc STP/μg of zircon; Humphreys et al.,
2004, Table I, p. 3) during the
initial heating phase to 500°C. As
shown in the following quotation, Humphreys et al.
(2003a, p. 13) feel that this partial
helium measurement is somehow compatible and supportive of
their revisions (see my Table 1) of
Gentry et al.'s (1982a) total helium
measurements:
"But as Appendix C reports, our experimenter Kenneth
Farley, not knowing how much he should find and going to
only 500°C, got a PARTIAL (NOT EXHAUSTIVE) YIELD of 540
nanomoles of helium per gram of zircon, or in Gentry's
units, 11 x 10-9 cm3/microgram
[note: the correct value as listed in Humphreys et al.,
2004, p. 3, is 12.1 x 10-9
cm3/microgram]. That is on the same order of
magnitude as Gentry's results in Table 2 [Humphreys et
al., 2003a], which reports the TOTAL (EXHAUSTIVE)
amount liberated after heating to 1000°C until no more
helium would emerge. Thus our experiments support Gentry's
data." [my emphasis]
Because the "540" nmol/g is only a partial helium
measurement and not a finalized total value, Humphreys et al.
(2004, p. 3) have no justification for even reporting
this value as an "approximation" in their Table 1 (that is,
~ 12.1 ncc STP/μg). Humphreys et al.
(2003a, p. 13) also have no rational reason for
comparing this incomplete analysis with revisions of Gentry
et al.'s data and then declaring that the
measurements "support" each other. The fallacy of this
comparison becomes very clear when all of the data in Table
C1 of Appendix C of Humphreys
et al. (2003a, p. 21) are reviewed. In the
table, heating steps 1-14 represent the initial temperature
increase to 500°C. If the nmol/g concentrations of
helium are summed for the 14 steps (5.337083... 171.5538),
the total amount of released helium is 864 nmol/g and
not 540 nmol/g. If the amount of helium
released by all 44 steps is summed, a total of 1794 nmol/g
is obtained. However, the cumulative fraction for step 44
in Table C1 is only 0.423501. By analogy with the biotite
analyses in Tables B1 and B2 in Humphreys et al.
(2003a, p. 18-19) and the zircon studies in Table II of
Humphreys et al.
(2004, p. 6), Farley must have obtained 57.6499% of the
total helium from the zircon sample during a fusion step.
This fusion step would have released 2442 nmol/g of helium
giving a grand total of 4236 nmol/g or 9.5 x
10-8 cc STP/μg (= 95 ncc STP/μg) of helium
from the sample.
Humphreys et al.
(2004, Table I, p. 3) claim that their 750-meter sample
has a Q/Q0 value of ~0.80, or ~12.1 ncc
STP/μg divided by Gentry's Q0 of 15
ncc STP/μg. However, the actual Q value for the
750-meter sample is 95 ncc STP/μg. Although
Q/Q0 values are always supposed to be one
or less, using Gentry's Q0,
Q/Q0 = 95 ncc STP/μg / 15 ncc
STP/μg = 6.3! My Q0 value from Appendix A (41 ncc STP/μg) still
yields Q/Q0 = 2.3. Q/Q0
values greater than one mean that the zircons have more
helium than expected.
The question then arises, why is Q/Q0
> 1 for the 750-meter sample? When determining Q,
did Farley analyze a group of exceptionally uranium- and
thorium-rich zircons? If so, these zircons could have had
Q0 >> 41 ncc STP/μg. As
discussed in Appendix B of this
report, uranium and thorium data from Gentry et al. (1982b)
are highly variable and suggest that Q0
values for the Fenton Hill zircons could be exceptionally
high in many cases. Even the uranium concentrations of the
three 750-meter zircons listed in Appendix A of Humphreys et al.
(2003a) show significant variations (that is, 218 to
612 ppm).
Another possible explanation for Q/Q0
> 1 is the presence of extraneous ("excess")
3He and 4He in the 750-meter zircons.
That is, have these zircons been contaminated with helium
from the mantle or surrounding locations in the crust? To
properly define the Q/Q0 values and
eliminate the possibility of extraneous helium, accurate
uranium, thorium, 3He, and 4He
analyses must be performed on the same
zircon grains. Any analyzed set of grains must also be
statistically representative of the zircon populations of
their host rocks. Furthermore, the zircons should be
collected from a freshly recovered
well-core and not from a core that has been stored under
unspecified surface conditions for more than 30 years.
Until all of these requirements are met, the
Q/Q0 values will remain poorly defined
and unable to support any of the "models" in Humphreys et al.
(2003a, p. 7-12; 2004).
EXTRANEOUS HELIUM IN THE BOREHOLE
SAMPLES?
As discussed in the previous section, extraneous helium
(3He and 4He) is one
possible explanation for the relatively high
Q/Q0 value of the 750-meter zircons.
Rather than properly considering the presence of extraneous
helium in their samples, it's obvious from their writings
that Humphreys et al. just assume that all of the
helium in their zircons is radiogenic; that is,
in-situ 4He from the radioactive decay of
the zircons' uranium and thorium. Although Humphreys et al.
(2003a, p. 3) claim that Gentry et al. measured
the amount of 4He in their samples, Gentry et al. (1982a)
clearly give no indication that they distinguished
extraneous 3He and 4He from
radiogenic 4He in any of their analyses. Simply
because of how zircons from samples 1-4 degassed, and
especially two groups from sample 4 with relatively
large (150-250 microns) specimens, Gentry et al. (1982a, p.
1130) thought that some of the helium in
samples 1-4 (Table 1) was radiogenic:
"That is, in the two deepest zircon
groups (3930 and 4310 m [samples 5
and 6]), we observed only short bursts of He (~1-2 sec) in
contrast to the prolonged 20 sec or more evolution of He
which was typical of He liberation from zircon groups down
to and including 3502 m [samples 1-4]. In fact, it was this
prolonged He liberation profile seen in two 150-250 micron
size zircon groups from 3502 m [sample 4] which convinces
us that SOME residual He is still trapped in the zircons
down to that depth (239°C)." [my emphasis]
Clearly, these degassing profiles did not quantify and
eliminate the possible presence of extraneous helium in the
relatively small (50-75 microns) zircons in samples 1-4,
which were used to derive Gentry et al.'s
Q/Q0 values. With respect to samples 5
and 6, Gentry et al.
(1982a, p. 1130) even admit:
"In fact, at present we are NOT certain whether the
minute amounts of He recorded from the deepest
zircons (3930 and 4310 m [samples 5
and 6]) are actually residual He in the zircons OR DERIVED
FROM SOME OTHER SOURCE." [my emphasis]
"Derived from some other source" would probably mean
extraneous helium or possible contamination from their
analytical procedures.
Extensive subsurface helium deposits occur in many parts
of New
Mexico, including sites in Union (Des Moines), San Juan
(Table Mesa), Harding (Bueyeros), Torrance (Estancia
Valley) and other counties. Additionally, the Fenton Hill
borehole site is located only about one kilometer from the
western boundary of the volcanic and helium-bearing Valles
Caldera (Sasada, 1989, p. 257).
The caldera formed between 1.45 and 1.12 million years ago
(Sasada, 1989, p. 257). The most
recent volcanism associated with the caldera occurred
roughly 130,000 years ago (Sasada,
1989, p. 258). Even YEC Vardiman (1990, p. 6) admits that
volcanic events may release helium. Clearly, Gentry et
al. and Humphreys et al. should have selected
samples from another area if they wanted to avoid the
possibility of extraneous helium contamination.
Significant 3He has been found in subsurface
fluids in the rocks of the Valles Caldera (sites Baca-4,
Baca-13, Baca-15, Baca-24, VC-2A and VC-2B; Goff and Gardner, 1994, p.
1816) only about 8 to 11 kilometers from the Fenton Hill
site (see the map in Figure 2 of Goff and Gardner, 1994, p.
1804-1805). In particular, geothermal fluids in the
Precambrian "granitoid" subsurface rocks at site VC-2B had
high R/RA values which ranged from 4.8 to 5.4
(Goff and Gardner, 1994, p.
1816), where R/RA =
3He/4He of the sample divided by
3He/4He of air. If
only 4He was present in the
fluids of the Baca and VC sites, the R/RA values
should have been zero. Goff and
Gardner (1994, p. 1816) and Smith and Kennedy (1985, p.
893) reasonably argue that the 3He enrichment in
the Baca and VC samples originated from sources in magmas
or the mantle.
Smith and Kennedy (1985,
p. 897) also indicate that 4He is currently
present in fluids from the Baca sites in concentrations
that range from 0.0183 cc/kg for Baca-15 to 0.1173 cc/kg
for Baca-4 (or 0.0183 to 0.1173 ncc STP/μg of extraneous
4He). According to Goff and Gardner (1994, p.
1816), wells Baca-15 and Baca-4 are greater than 1,000
meters deep and have bottom temperatures of 267°C and
295°C, respectively. The nearby Fenton Hill rocks could
also easily contain at least 0.01 ncc STP/μg of
extraneous helium. Unless Humphreys et al. can
thoroughly identify and subtract out any extraneous
background helium, no one should expect realistic results
from the "creation" and "uniformitarian models" (for
example, the extremely small Q/Q0 values
predicted by the "uniformitarian model" in Table 5 of
Humphreys et al., 2003a, p. 12 could be easily
masked by extraneous helium).
YECs often improperly claim
that "undetected excess" (extraneous) argon (see
definitions in McDougall
and Harrison, 1999, p. 11) nullifies K-Ar and Ar-Ar
dating. Certainly, extraneous argon has been known to
contaminate some minerals (Faure,
1986, p. 72). AiG is also swift to tell their readers
that
diamonds
may be contaminated with "excess" (extraneous) argon (also
see Faure, 1986, p. 72). Because
helium atoms are much smaller than argon atoms, they would
tend to more readily move in and out of most minerals than
argon. So, if YECs enthusiastically accept the existence of
extraneous argon, why shouldn't they acknowledge that
subsurface minerals (including zircons) could be
substantially contaminated with extraneous helium?
If extraneous helium is present in the Fenton Hill
zircons, at least 3He might be identified and
appropriate corrections could be made. Furthermore, there
are techniques for identifying extraneous ("excess") argon
(Hanes, 1991; McDougall and Harrison,
1999, p. 114-130) and analogous methods might be able
to identify extraneous 4He. Quartz and other
impermeable and low uranium minerals should also be
analyzed for extraneous helium. If extraneous helium occurs
in quartz, it's probably also present in adjacent zircons.
So, before Humphreys et al. can use their "studies"
to promote their religious agenda, they clearly need to
measure the R/RA values of fresh (not >30
years old) samples and eliminate any possible effects from
extraneous helium.
In response to the possibility of extraneous helium in
their zircons or claims by their critics that high helium
concentrations could exist in the biotites surrounding
their zircons, Humphreys
et al. (2003a, p. 13) state:
"A second uniformitarian line of defense might be to
claim that the helium 4 concentration in the biotite or
surrounding rock is presently about the same as it is in
the zircons. (Such a scenario would be very unusual,
because the major source of 4He is U or Th
series radioactivity in zircons or a few other minerals
like titanite or apatite, but not biotite.) The scenario
would mean that essentially no diffusion into or out of the
zircons is taking place. However, our measurements
(Appendix B) show that except for possibly samples 5 and 6,
the concentration of helium in the biotite [sect. 6,
between eqs. (7) and (8)] is much lower than in the
zircons. Diffusion always flows from greater to lesser
concentrations. Thus helium must be diffusing out of the
zircons and into the surrounding biotite."
Obviously, Humphreys et al. have an invalid
Lyell uniformitarian mindset that YECs so often accuse
scientists of possessing. That is, Humphreys et al.
falsely believe that if the helium concentrations in
"surrounding" biotites are now relatively
low, then these concentrations must have
always been low. Humphreys et al.
fail to realize that the zircons may have been contaminated
with extraneous helium many thousands of years ago. Since
then, the extraneous helium could have largely dispersed
from the biotites and other relatively permeable minerals.
However, it may still remain trapped at
10‑8 to 10‑11 cc
STP/μg in relatively impermeable zircons. Also rather
than always penetrating the zircons, helium pressures
surrounding the minerals may have been periodically high
enough in the past to temporarily prevent or extensively
slow down the escape of any helium from the zircons.
SOME GENERAL DIFFUSION ISSUES
Helium Solubility in Zircons, "Interface
Resistance" and Open Systems
In response to an unknown critic, Humphreys et al.
(2004, p. 12-14) argue that "interface resistance" and
helium solubility in zircons are not significant enough to
hinder the flow of helium out of their
zircon samples. As explained above, the Jemez Granodiorite
(Zartman, 1979) and the
overlying gneiss (Appendix A in Humphreys et al.,
2003a) have discordant U/Pb dates, which indicate open
system behavior for lead and/or uranium, and no doubt
helium. Open systems not only mean that helium may
periodically flow out of zircons, but if the helium
pressures surrounding the minerals were once higher,
extraneous helium could have periodically flowed
into them. To enter a zircon, extraneous
helium need not actually dissolve into the zircon
crystalline structure or readily migrate across the
boundary (interface) between a biotite and zircon crystal.
The helium could have entered and become trapped in
fractures, permeable metamict areas and other significant
voids in the zircons. Again, such event(s) could explain
the high helium values in the 750-meter zircons.
Fudging Old and Ambiguous Soviet
Data
Humphreys et al.
(2003a, p. 6 and 2004, p. 2) cite Magomedov (1970), a Soviet paper
which contains some early data on helium diffusion in
zircons. Only a brief abstract of Magomedov (1970) is readily
available in English:
"Heating experiments at 1000 and 1150°C and up to 48
hours on zircon suggest loss of surface lead and helium is
considerable during the first few hours. Estimates of
activation energy of bulk diffusion are 58 kcal/mole for Pb
in zircon, and only 15 kcal/mole for He."
Humphreys, however, has an English translation of the
entire article (Humphreys
et al., 2003a, p. 16).
Humphreys et al.
(2003a, p. 6) describe a graph in Magomedov (1970) and reproduce it
in their Figure 5 (p. 6). The y-axis of the graph in Magomedov (1970) has units of
"ln(D,σ)," where D refers to the
diffusion coefficient and σ represents electrical
conductivity, which may influence diffusion in some
crystals according to an old reference, Girifalco (1964, p. 92-102).
Based on Reiners et al.'s
(2002) results on helium diffusion in zircons from the
Fish Canyon Tuff, Humphreys
et al. (2003a, p. 6) conclude that the units on
Magomedov's graph must be "incorrect" and that the actual
units should be log base 10 D (log10
D). However, Magomedov's zircons were very metamict;
that is, severely damaged by radiation probably from high
uranium concentrations. Considering the conditions of the
samples and the fact that different specimens of the same
mineral may have significantly dissimilar physical and
chemical properties, the high helium diffusion coefficients
in Magomedov (1970) could be
real and Humphreys et
al. (2003a) may not be justified in "correcting"
the Soviet data. Very different helium diffusion rates
would be expected, especially when highly metamict zircons
are compared with essentially non-metamict specimens or if
comparisons are made between high- and low-helium zircons.
While Humphreys et al.
(2003a, p. 6) boast that their log10D
interpretation of the Soviet data is still five orders of
magnitude too high for their "uniformitarian model," they
forget to mention that before they "corrected" the Magomedov (1970) data, these
Soviet results were at least five orders of magnitude
higher than their “Jemez” measurements and the
Fish Canyon Tuff data in Reiners
et al. (2002).
Instead of altering the Magomedov (1970) data in
their (2003a) Figures 5 (p. 6) and
6a (p. 7), Humphreys et al. should have remembered
their own pronouncement
(2003a, p. 6):
"Measurements of noble gas diffusion in a given type of
naturally occurring mineral often show significant
differences from site to site, caused by variations in
composition."
The data in Magomedov
(1970) are 35 years old and Humphreys et
al. (2003a, p. 1, 6) and Humphreys et al.
(2004, p. 2) are certainly correct when they describe
the data as ambiguous. Humphreys et al.
(2003a) should have simply ignored these questionable
results rather than adjusting the units to fit data from Reiners et al. (2002)
and ultimately their own results (Figure 6a in Humphreys et al.,
2003a, p. 7).
Arrhenius Plots in Humphreys et
al.: Fictional Knees and Imaginary Defect Lines
Arrhenius graphs describe how diffusion coefficients
change with temperature under laboratory conditions (Humphreys et al.,
2003a, p. 5; their Figures 4a and 4b). Quoting Girifalco (1964, p. 102, 126), Humphreys et al.
(2003a, p. 5) argue that Arrhenius plots "typically"
consist of two different-sloping lines connected by a
"knee." Because zircons and most other minerals have
fractures, impurities, dislocated atoms, and other defects
in their crystalline structures, Humphreys et al.
(2003a, p. 5, 7; their Figure 4) expect "knees" and
shallow-sloped defect lines to appear at lower temperatures
on most Arrhenius plots. For example, Humphreys et al.
(2003a, p. 7) claim:
"Because the New Mexico [Fenton Hill] zircons are
radioactive, they must have some defects and should have a
knee at some lower temperature than 300°C."
Although almost all natural crystals contain
considerable impurities and other defects, these features
may not always produce "defect lines" on Arrhenius plots as
Humphreys et al.
(2003a, p. 5, 7) expect. The Arrhenius plots may be
fairly linear, like the examples with the Fish Canyon Tuff
zircons in Reiners et al.
(2002), other silicate minerals in Lippolt and Weigel (1988), or
even Humphreys et al.'s
(2003a; 2004) actual data as shown in my Figure 1. Girifalco (1964, p. 100-102, 124,
126) mentions that impurities in
ionic crystals (like halite ["table
salt"]) and polycrystalline (multiple,
usually intergrown, crystals) samples may produce
"extrinsic" curves (that is, "knees" and "defect lines"
like in Figure 4a of Humphreys et al., 2003a, p. 5).
Because the descriptions in Appendix C of Humphreys et al.
(2003a, p. 20) indicate the presence of single crystal
(not polycrystalline) zircon grains and not overly
excessive metamict features, significant knees and defect
lines may not be present.
Figure 1. An Arrhenius plot of Humphreys et
al.'s (2003a; 2004) zircons from
gneiss samples collected at depths of 750 and 1490 meters
from the Fenton Hill core. 330°C = 1.66 1000/Temp
(Kelvin), 197°C = 2.13 1000/Temp (K) and 175°C =
2.23 1000/Temp (K).
 |
A knee and a defect curve are visible in Figure 5 of Humphreys et al.
(2003a, p. 6) for the exceptionally metamict Soviet
zircons. However, Humphreys
et al. (2003a, p. 7) admit:
"At 390°C (abscissa = 1.5), the Russian data have a
knee, breaking off to the right into a more horizontal
slope for lower temperatures. That implies a high number of
defects (see sect. 4), consistent with the high radiation
damage Magomedov reported. The Nevada and New Mexico data
go down to 300°C (abscissa = 1.745) with no strong
knee, implying that the data are on the intrinsic part of
the curve."
Measurements in Humphreys
(2003) and Humphreys et al. (2004, Table II, p.
6) extend down to 175°C, but were performed on zircons
from depths of 1490 meters rather than 750 meters. Now,
Figure 6 in Humphreys et
al. (2004, p. 7) might show a
slight "knee" at about 1.75 =
1000/T(Kelvin) (approximately 300°C), which happens to
correspond to the lowest temperature measurement on the
750-meter zircons (also see my Figure 1). However, contrary
to the following prediction from Humphreys et al.
(2003a, p. 7), no obviously sharp knee resembling the
one in the Soviet data is present on Humphreys et
al.'s curve:
"Because the New Mexico zircons are radioactive, they
must have some defects and should have a knee at some lower
temperature than 300°C."
In the figure on p. iii of Humphreys (2003) and Figure 6 of
Humphreys et al.
(2004, p. 7), Humphreys et al. draw a "sharp
knee" at about 197°C (1000/T(K) =
2.13) as part of a two-sloped curve generated by their
"creation model." However, once the "creation model curve"
is removed from their figures (also, see my Figure 1), no
obvious knee is visible in the actual data. Careful
observations of the actual zircon data in Humphreys et
al.'s figures (also see my Figure 1) only show a
continuing slightly parabolic trend without any obviously
sharp knee or defect line.
Lippolt and Weigel
(1988, p. 1452-1454) also contains a number of
4He Arrhenius plots for different minerals,
including sanidine, nepheline, hornblende, pyroxenes,
langbeinite, and muscovite. Rather than having knees and
defect lines, many of the data are linear to almost
200°C and Lippolt and Weigel extrapolate all of the
data as straight kneeless lines down to 20°C. Clearly,
Lippolt and Weigel (1988),
Reiners et al. (2002)
and other researchers do not consider defect lines to be
common features on their Arrhenius plots. Because defect
lines and knees are often absent on Arrhenius plots of
helium diffusion in silicate minerals (Lippolt and Weigel, 1988; Reiners et al., 2002),
there is no certainty that samples 1 and 2 will lie on
defect lines as shown in the "creation" and "uniformitarian
models" in Figure 8 of Humphreys et al.
(2003a, p. 11) or Figure 6 in Humphreys et al.
(2004, p. 7). Furthermore, because defect lines are not
always expected, "WeHappyFew" correctly noticed that the
following diffusion coefficient (D1) and
exceptionally low activation energy (E1)
(equation 18, p. 13 of Humphreys et al., 2003a)
"predicted" by the "defect line" of the Humphreys et al.
(2003a) "creation model" have no evidence of
existing:
E1 ~ 3.76 kcal/mole,
D1 ~ 7.4 x 10-14
cm2/sec
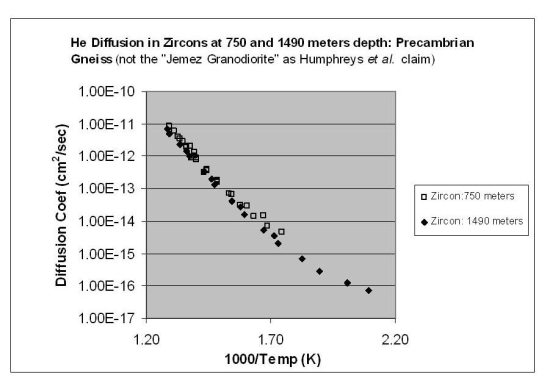
In another example of imaginary defect lines, Figure 6b
of Humphreys et al.
(2003a, p. 7) shows muscovite concentrate data from Lippolt and Weigel (1988, p.
1454) (also see my Figure 2). The lower temperature portion
of the data has a scattering of several points. Lippolt and Weigel (1988, p.
1452, 1455) attribute the scatter to uneven distributions
of uranium in the muscovite grains and do not mention the
possibility of defect lines on their Arrhenius plot. They
simply fit a straight line through the scatter and admit
that these muscovite diffusion and activation energy
results are not quantitative. Rather than faithfully
representing Lippolt and Weigel's results, Humphreys et al.
(2003a, p. 7) omit Lippolt and Weigel's best-fit linear
curve and selectively connect some of the lower temperature
points in their Figure 6b (also see my Figure 2). The lines
in Humphreys et al.'s Figure 6b suggest the presence
of a "knee" and "defect line" that Lippolt and Weigel (1988)
never intended (compare my Figure 2 and Humphreys et
al., 2003a, Figure 6b, p. 7).
Figure 2: Arrhenius plot of muscovite data from Lippolt and Weigel (1988, p.
1454) and their linear best-fit curve. In their Figure 6b,
Humphreys et al.
(2003a, p. 7) remove the Lippolt and Weigel best fit
line and selectively connect some of the data points, which
create false impressions that a "knee" and "defect line"
are present.
 |
Lead Diffusion
Using information from Nicolaysen (1957) and Magomedov (1970) in footnote 16
of Gentry et al.
(1982b, p. 298), Humphreys
et al. (2004, p. 10) performed some calculations
and claimed that 60-micron long zircons (a = 30
microns) from sample 6 should lose about 50% of their lead
if they were exposed to 313°C for 1.5 billion years.
Because the zircons supposedly still have about 90% of
their lead (Humphreys et
al., 2004, p. 9), Humphreys et al.
(2004, p. 10) spuriously argue that the zircons must be
much younger than 1.5 billion years old.
Using measurements from a 1979 report by Zartman, Ludwig et al. (1984)
argue that zircons from approximately 2900 meters (sample
3; Table 1; only 197°C in 1974) have lost about 25% of
their lead (also see Gentry,
1984). Considering that the lead loss from the zircons
of sample 3 is significant, the deeper and warmer zircons
in sample 6 have probably experienced greater lead losses
than what Humphreys et
al. (2004, p. 9-10) want us to believe.
More recent activation energy (161 kcal/mol) and
temperature-independent diffusion coefficient
(approximately 3.9 x 109 cm2/sec)
values for lead in zircons are listed in Lee et al. (1997, p. 160,
161). These values are very different from the older
measurements in Nicolaysen
(1957) and Magomedov
(1970). Inserting the values from Lee et al. (1997) into the
equations of footnote 16 in Gentry et al. (1982b)
yields results that predict insignificant lead diffusion
losses in zircons at ≤ 313°C over 1.5 billion years
(about 1% predicted lead loss at 313°C rather than
approximately 50% as claimed by Humphreys et al.,
2004, p. 10). A 25% actual lead loss in the sample 3
zircons or any significant losses in the zircons of deeper
samples could be explained by the presence of metamorphic
fluids and/or prolonged exposure to temperatures well above
313°C sometime in the distant past. Rather than deal
with reasonable possibilities, Humphreys et al.
(2004) use outdated measurements and make fallacious
assumptions, which cause them to erroneously conclude that
the lead data are incompatible with an ancient age for the
zircons.
Although zircons in the Fenton Hill core may have lost
considerable lead, typically Pb-Pb dates would not be
significantly affected (Ludwig
et al., 1984; Faure,
1998, p. 288). The masses of the lead isotopes are so
similar (204, 206, 207 and 208 amu) that loss events would
not be able to remove more of one lead isotope than
another.
MAJOR ASSUMPTIONS, INCONSISTENCIES AND
OTHER PROBLEMS IN THE HUMPHREYS ET AL. "MODELS"
Some Major Assumptions in Humphreys et
al.'s "Models"
Because precise data may not always be available or
natural conditions may be too complex to be thoroughly
deciphered, scientists must often make assumptions and
compromises in order to develop functioning models. These
unavoidable assumptions and compromises will often reduce
the accuracy of the models. Obviously, when making
assumptions, scientists must be very careful not to
generate models that produce deceptively erroneous
results.
Humphreys et al.
(2003a) make several assumptions when developing and
applying their "models." In addition to the previously
mentioned examples, other major assumptions are listed
below and discussed. As demonstrated in the following
paragraphs, some of these assumptions are entirely
unreasonable.
Assumption #1: Laboratory Vacuum Diffusion Results
Accurately Model Diffusion under Relatively High Pressure
Subsurface Conditions.
A major assumption of Humphreys et al.'s work is
that diffusion measurements obtained under a laboratory
vacuum can accurately estimate natural diffusion rates at
depths of 750 - 4310 meters in the subsurface (about 200 to
1,200 bars of pressure; Winkler,
1979, p. 5. Note: Average atmospheric pressure
is about 1 bar.). Obviously, helium will more readily degas
from a bare zircon in a rapidly heated laboratory vacuum
than a deep subsurface zircon that is surrounded by
minerals and high-pressure fluids. Furthermore, vacuums may
decompose minerals (such as biotites and other micas) or
open fractures, which would allow helium to more readily
escape than under natural subsurface conditions.
Farley (2002, p. 822)
warns that laboratory diffusion data must be carefully applied to natural
situations:
"It is important to note that such laboratory measurements may not apply under
natural conditions. For example, diffusion coefficients are commonly measured
at temperatures far higher than are relevant in nature, so large and
potentially inaccurate extrapolations are often necessary. Similarly, some
minerals undergo chemical or structural transformations and possibly defect
annealing during vacuum heating; extrapolation of laboratory data from these
modified phases to natural conditions may lead to erroneous predictions."
Lippolt and Weigel
(1988, p. 1451) also question whether laboratory vacuum
experiments adequately model the degassing behavior of
certain minerals under natural conditions. These issues
must be kept in mind when evaluating Humphreys et
al.'s "models," especially with their biotite data.
Assumption #2: Constant Temperatures over
Time.
Harrison et al.
(1986) and Sasada (1989)
clearly refute a major assumption in Humphreys et al.
(2003a, p. 8), which states that subsurface
temperatures at Fenton Hill have been constant over time.
Using 40Ar/39Ar dates from feldspars
at depths of 1130, 2620, and 2900 meters in the Fenton Hill
core samples, Harrison et
al. (1986, p. 1899, 1901) concluded that the
temperatures for these samples fell below approximately
200°C about 1030 million years ago and below about
130°C around 870 million years ago. Harrison et al. (1986,
p. 1899) also identified a noticeable thermal event in the
Fenton Hill core samples within the past few tens of
thousands of years.
Figure 9 in Sasada (1989, p.
264) shows the variable thermal history of the GT-2 well
core at a depth of 2624 meters (compare with my Figure 3).
According to Sasada (1989, p.
262-265), a warm period occurred sometime ago. Even hotter
earlier events could have removed much or even essentially
all of the radiogenic helium from the zircons. The warm
period was followed by a cooler event,
which included the emplacement of fluids (see my Figure 3).
In particular, Sasada (1989)
argues that fluids were trapped in secondary inclusions
within the Jemez Granodiorite at depths of 2624 meters when
temperatures were at least 26°C cooler
than present (about 152°C rather than the current value
of 178°C). Sasada (1989, p.
265) does not provide any definitive dates for the heating
and cooling events, but he argues:
"The fluid inclusions in the calcite veins and those in
quartz of the Precambrian crystalline rocks from the GT-2
indicate heating up to the thermal maximum, cooling and
calcite veining, and heating again to the present
temperature."
Obviously, these fluids could have contained extraneous
helium. During prolonged exposure, the helium could have
contaminated biotites, zircons and other minerals. The
cooling event was then followed by reheating to present
temperatures. During this current reheating event, the
cleavage planes in biotites and other micas would provide
excellent pathways for their extraneous helium to largely
dissipate as background helium concentrations in the
regional crust declined. However, the relatively
impermeable zircons could have retained any extraneous
helium for a longer period of time, perhaps up to the
present. Therefore, instead of observing the substantial
remnants of radiogenic helium in zircons from 1.5 billion
years' worth of uranium and thorium decay, Humphreys et al.
(2003a,b) may be largely analyzing remaining extraneous
helium that contaminated the Fenton Hill subsurface rocks
during relative cool periods in the recent past. Now,
Humphreys et al. might scoff at my extraneous helium
hypothesis, but at least it's a valid and testable
scientific hypothesis and not a supernatural religious
excuse to get rid of undesirable evidence. Again, Humphreys
et al. should be able to confirm or refute the
presence of extraneous helium by looking for 3He
in zircons and 4He in low uranium and thorium
minerals from fresh Fenton Hill samples.
Figure 3. Thermal history of Fenton Hill Jemez
Granodiorite at 2624 meters depth and hypothetical
relationships with extraneous helium (based on Figure 9 in
Sasada, 1989).
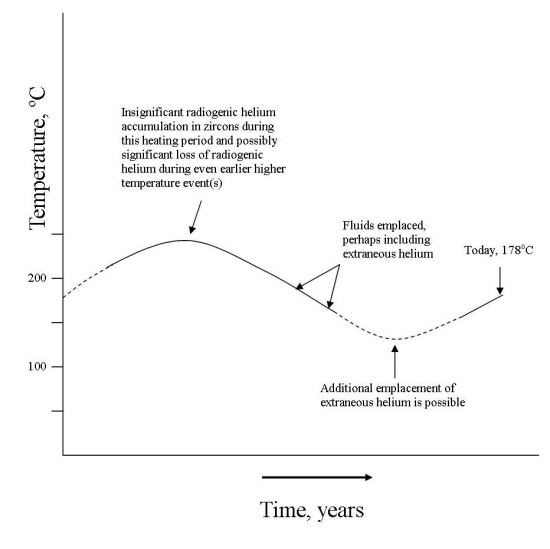 |
When discussing their "uniformitarian model," Humphreys et al.
(2003a, p. 10) admit that the Fenton Hill samples have
had a variable temperature history, which includes both
relatively warm and cool periods. Nevertheless, as Humphreys et al.
(2003a, p. 10; 2004, p. 8) discuss the thermal history
of the Fenton Hill region, they ignore the importance of
cooler periods when high fluid pressures could have
hindered the diffusion of helium from the zircons and
perhaps even contaminated them with extraneous helium.
Whatever the history of the helium in the zircons, it is
utterly improper for Humphreys et al. to construct a
strawperson constant-temperature "uniformitarian model" for
these minerals. The 1.5 billion year-old history of these
minerals is obviously too complex for such a simplistic
approach. Because of this complex thermal history, Humphreys et al.
(2003a, Section 10, p. 13-14) also have no
justification for describing the current helium
concentrations in the zircons with one simple "closure
interval."
In response to the reality of a variable thermal history
for the Fenton Hill area (my Figure 3), Humphreys et al.
(2003a, p.10; 2004, p. 8) simply claim that they
assumed constant temperatures over time to be "generous" to
the "uniformitarians" and that without constant
temperatures, the "uniformitarian model" would be even
worse. However, accuracy is always more important than
adopting obviously false strawperson
assumptions just to be "generous" to your opponents.
Scientists don't need or want any erroneous "acts of
generosity" from Humphrey et al. If a problem
exists, scientists must deal with it realistically.
Meanwhile, until better data are obtained, Humphreys et
al. have no rational grounds for quoting their Bibles
and invoking
"god-of-the-gaps" to explain away the history of these
zircons.
Assumption #3: Biotites Encapsulate the
Zircons.
The Humphreys et
al. (2003a, p. 8) "creation model" considers the
diffusion of helium through both zircons and biotites. They
assume that the zircons were largely surrounded by
biotites, which may be true. Of course, zircons can also
occur in other minerals. For example, in some gneisses,
zircons are common in cordierite, a metamorphic mineral (Perkins and Henke, 2004, Plate
32a,b).
Assumption #4: Isotropic Diffusion in
Zircons.
In their modeling efforts, Humphreys et al.
(2003a, p. 8; their Figure 7) assume that helium
diffusion in zircons is isotropic; that is, spherical. Of
course, zircons have tetragonal (anisotropic) rather than
isotropic crystalline structures, which would cause some
anisotropy in the flow of helium through the minerals.
Although scientists may assume spherical diffusion in
zircons to simplify calculations (e.g.,
Reiners
et al., 2002, p. 300-301), the assumption is not
strictly true and could introduce at least minor errors
into Humphreys et al.'s "models." Humphreys et al.
(2004, p. 15) attempt to minimize the problem by
claiming that switching the diffusion geometry of zircons
from an isotropic sphere to an anisotropic cylinder would
change their results by less than a factor of two. However,
they provide no detailed calculations to support this
claim.
Assumption #5: Isotropic Diffusion in
Biotites.
Although assuming spherical (isotropic) diffusion in
zircons may be a reasonable approximation, helium diffusion
in biotite is definitely anisotropic. Biotite consists of a
series of parallel or semi-parallel cleavage planes. Helium
would preferentially migrate through the well-defined
cleavage planes rather than undergoing equal dispersion in
all directions (spherical dispersion). Although Humphreys et al.
(2003a, p. 8) recognize that helium diffusion is
anisotropic in biotites, they inappropriately assume
isotropic diffusion in the micas to simplify the
mathematics of their "creation" and "uniformitarian
models":
"Diffusion in biotite is not isotropic, because most of
the helium flows two-dimensionally along the cleavage
planes of the mica. But accounting for anisotropy in the
biotite would be quite difficult, so we leave that
refinement to the next generation of analysts. To keep the
mathematics tractable, we will assume spherical
symmetry..."
Because of the prominent cleavage planes in biotites,
this shortcut in their "modeling" approach is totally
unjustified and could lead to very inaccurate and deceptive
results. In particular, almost all of the equations and
results on pages 8-14 of Humphreys et al.
(2003a) are based on this grossly invalid assumption.
Clearly, because of this and other false assumptions (such
as, constant temperatures; Assumption #2), the equations
and their results and "models" are unrealistic and cannot
be trusted. Humphreys et al. should have waited for
reliable results from the "next generation of
analysts."
The fictional isotropic "creation model" is illustrated
in Figure 7 of Humphreys
et al. (2003a, p. 8), where a shell representing
isotropic diffusion in biotite surrounds a sphere
representing isotropic diffusion in a zircon. Rather than
surrounded by a "shell" of isotropic biotite, a group of
real-world zircons might lie within biotite cleavage planes
and distort the shape of the planes, which would further
complicate helium diffusion. In another likely scenario, a
larger zircon could easily cross several cleavage planes.
Any helium escaping from this cross-cutting zircon could
flow into several biotite cleavage planes.
Assumption #6: Biotite and Zircon have the Same
Diffusion Coefficients.
To further simplify the mathematics of their "models,"
Humphreys et al.
(2003a, p. 9) assume that the diffusion coefficients of
the zircons and surrounding biotites were the same. Humphreys et al.
(2003a, p. 9; 2004, p. 15) argue that this assumption
would shorten the diffusion times by no more than 30%.
Because they believe that their ages would be lengthened by
this assumption, Humphreys et al. argue that
"uniformitarians" should not object to this assumption.
However, considering the complexities of helium flow through deformed biotite
cleavage planes, variable fluid pressures over time, and many other
uncertainties, the errors could be much greater than 30%.
Assumption #7: Measurements of b from Biotites
Apply to at Least Samples 3-5.
Although already collapsed by biotite anisotropy, the
foundation of the "creation model" further disintegrates
because Humphreys et
al. (2003a, p. 8) fail to indicate how many biotite
grains were measured to obtain b (the radius of the
biotite supposedly surrounding each zircon as shown in
their Figure 7). Without providing any standard deviations,
Humphreys et al.
(2003a, p. 8) simply claim that the biotite flakes in
the "Jemez Granodiorite" average about 0.2 millimeter in
thickness and approximately 2 millimeters in "diameter."
Based on these data, Humphreys et al.
(2003a, p. 8) then conclude that b ~ 1000 microns and
that this value is applicable when calculating "dates" for
samples 3-5 (equations 14a-c and 17, Humphreys et
al., 2003a, p. 9-12). Of course, if their measurements
were done on biotites from the 750 meter-deep gneiss, the
results may not even approximate the sizes of the biotites
in the Jemez Granodiorite of sample 3 and the lithologies
(Jemez Granodiorite?) in samples 4 and 5.
Why did Humphreys et al. Treat
Sample 6 Differently than Sample 5?
"Ordinary" Diffusion in Samples 1-5?
To develop and promote their "creation model," Humphreys
et al. must explain the helium distributions in the
Fenton Hill core samples and demonstrate that their
diffusion data are only consistent with a 6,000 year old
time span. While reviewing their data, Humphreys et
al. readily noticed that the Q and
Q/Q0 values of samples 1-5 seem to
consistently decrease with depth and increasing subsurface
temperatures (see my Table 1). Humphreys et al.
attribute this inverse relationship between
Q/Q0 values and temperature to "ordinary
diffusion." As Humphreys
et al. (2003a, p. 4) state:
"Getting back to the helium data, notice that the
retention levels [Q/Q0 values] decrease
as the temperatures increase. That is consistent with
ordinary diffusion: a high concentration of helium in the
zircons diffusing outward into a much lower concentration
in the surrounding minerals, and diffusing faster in hotter
rock. As the next section shows, diffusion rates increase
strongly with temperature."
Humphreys et al.
(2003a, p. 3) recognize that the helium concentration
(~2 x 10-11 cc STP/μg) in sample 5 "agrees"
with the temperature and helium concentration "trends" in
samples 1-4, but that an identical helium measurement from
sample 6 is "too high" to fit their "model." To validate
their "creation model," Humphreys et al.
(2003a, p. 3, 8) must demonstrate that the Q and
Q/Q0 values for sample 5 are trustworthy
and should be included in their "models." At the same time,
Humphreys et al. must think of some excuse to treat
the identical results from sample 6 as a "special case" and
somehow eliminate them from the "modeling" efforts.
As previously discussed, Humphreys et al.
(2003a, p. 3) fail to realize that samples 1-5 come
from different rocks types (see my Table 1) and that the
Q/Q0 values of these different samples
should not be compared. In an analogous situation involving
their surface and sample 1 (960 meters deep) zircons, Gentry et al. (1982a, p.
1130) correctly warn about comparing the
Q/Q0 values of samples from different
lithologies:
"The near equality of the He concentrations in the
surface and 960 m depth zircons [see my Table 1] is NOT
particularly meaningful because the surface zircons were
from an ENTIRELY DIFFERENT geological unit and DOUBTLESS
HAVE DIFFERENT U-Th-Pb concentrations than the zircons from
the core samples." [my emphasis]
Now, the helium concentrations in samples 1-5 may indeed
result from relatively simple diffusion through several
different lithologies in the crust. However, before
Humphreys et al. or anyone else can conclusively
endorse this claim, they must realize that the variable
chemistry and lithologies in the Fenton Hill cores could
provide other possible explanations for the supposed
decrease in Q/Q0values with depth. For
example, the chemical data in Gentry et al. (1982b)
(also shown in Table B1 of my Appendix
B and my Table 3) suggest that the zircons from sample
1 are enriched in uranium and thorium when compared with
most of the zircons in samples 5 and 6. Because uranium-
and thorium-rich zircons would tend to have higher helium
(Q) concentrations, applying a constant
Q0 value of 15 ncc STP/μg to zircons
with variable uranium and thorium concentrations (as Gentry
et al., 1982a and Humphreys et al., 2003a,
2004 did) could generate a series of fictitious
Q/Q0 values with very deceptive trends.
Clearly, Humphreys et al. must provide suitable
Q/Q0 values and supporting data to
definitively demonstrate helium diffusion and rule out
other scenarios.
How Reliable are the Results from Samples 5 and
6?
Rather than being quantitative or even semiquantitative
helium measurements (Q) as Humphreys et al.
(2003a) believe, the results for samples 5 and 6 could
largely represent contamination or other types of
interference from Gentry et al.'s
(1982a) analytical equipment. This is probably why Gentry et al. (1982a, p.
1130) listed the values as only approximations. It's also
possible that both the helium in samples 5 and 6 are
entirely extraneous background concentrations that resulted
from regional volcanic activity sometime in the recent
geologic past (Harrison et
al., 1986). As stated before, Gentry et al. (1982a, p.
1130) admit that the low concentrations of helium in the
zircons of these samples may not be in-situ
radiogenic 4He:
"In fact, at present we are NOT certain whether the
minute amounts of He recorded from the deepest
zircons (3930 and 4310 m
[i.e., samples 5 and 6]) are actually residual He in
the zircons OR DERIVED FROM SOME OTHER SOURCE.
[e.g., extraneous helium or analytical
interferences]" [my emphasis]
Although Humphreys et
al. (2003a, p. 3) claim that they will "allow for
the possibility" that the error on the helium measurement
of sample 5 is considerably larger than the errors of
samples 1-4, their Table 1 lists no error for the
Q/Q0 value of sample 5 and they generally
treat the helium concentration of the sample in a
quantitative manner in their models (as examples, Tables 4
and 5 in Humphreys et
al., 2003a, p. 12). The semiquantitative (at best)
nature of the helium (Q) results for samples 5 and 6
must be remembered when evaluating helium diffusion
"dates."
Are the Helium Distributions in Sample 6 Uniform?
What about Sample 5?
Rather than treating both samples 5 and 6 as
contamination during analysis, unreliable instrument noise,
minor helium background concentrations, or in another
consistent manner, Humphreys
et al. (2003a) attempt to justify eliminating
sample 6 from their "models." At the same time, they fail
to apply the same standards to sample 5. Specifically, Humphreys et al.
(2003a, p. 8) make the following ambiguous
arguments:
"Because b is more than 32 times larger than
a, the disk-like (not spherical) volume [sic]
of biotite the helium enters is more than 1000 (~32
squared) times the volume of the zircon. This consideration
affects the boundary conditions we choose for r =
b, and how we might interpret sample 6 (see sect.
2), as follows. [new paragraph] Suppose that helium could
not escape the biotite at all. Then as diffusion proceeds,
C would decrease in the zircon and increase in the
biotite, until the concentration was the same throughout
the two materials. After that C would remain
essentially constant, at about 0.001 C0.
The fraction Q/Q0 remaining in the zircon
would be about 0.001, which is just what Gentry observed in
sample 6."
Humphreys et al.'s statements are certainly very
vague. What is meant by "disk-like volume"? How can Humphreys et al.
(2003a, p. 8) say: "...the disk-like (not spherical)
volume of biotite the helium enters is more than 1000 (~32
squared) times the volume of the zircon,
[my emphasis]" when volumes have three dimensions and not
two? (That is, cubed and not squared
dimensions.) If Humphreys et al. are trying to
compare a and b by passing a random plane
through the center of a zircon and into its surrounding
biotite, how can C ~ 0.001 C0 since the plane
would probably intersect several other zircons that are
additional sources of helium? Perhaps, Humphreys et
al. are suggesting in their statements that all of the
helium diffusing out of a sample 6 zircon enters into only
one apparently two-dimensional "disk-like" biotite cleavage
plane. If so, as shown in the following calculations, the
"disk-like" volume of one cleavage plane
in their biotites is not 1000 times the
spherical diffusion volume of an a = 30 microns
zircon crystal. On the very unlikely scenario that the
helium from a zircon could somehow only flow into
just one biotite cleavage
plane, then the following
volume comparisons would be obtained with
the Humphreys et al. data:
a of Zircon = 30 microns. Assuming isotropic
diffusion of helium in zircons. Spherical diffusion volume
of the zircon = 4/3πa3 =
4/3(3.141)303 = 113,000 cubic microns in a
relatively impermeable mineral.
IF all of the helium from the zircon
enters only one biotite cleavage plane (the typical width
[h] of a biotite cleavage plane is about 3.4 Å
[0.00034 microns]; Bailey, 1984,
p. 20-23), then Humphreys et al.'s
(2003a, p. 8) disk-like volume would
be:
V = πb2h =
3.141(1000)2(0.00034) = 1070 cubic microns
(generally permeable volume).
When comparing the two volumes, the results are much
less than the 1,000 times claimed by Humphreys et al.
(2003a, p. 8):
Vbiotite / Vzircon = 0.0095
So the diffusion volume of Humphreys et al.'s
biotite cleavage plane is only about 0.0095 times that of
an a = 30 microns zircon. Of course, helium
diffusion in biotites is faster than in zircon because
zircon is relatively impermeable and does not contain
regular cleavage planes. Furthermore, any helium would
probably migrate through multiple and relatively permeable
cleavage planes in biotites. Because of their erroneous and
unrealistic statement that "... the disk-like (not
spherical) volume of biotite the helium enters is more than
1000 (~32 squared) times the volume of the zircon," Humphreys et al.
(2003a, p. 8) cannot claim that "The fraction
Q/Q0 remaining in the zircon would be
about 0.001, which is just what Gentry observed in sample
6." So, Humphreys et
al. (2003a) must come up with another excuse to
remove sample 6 from their “models.”
Because of their invalid zircon and biotite "volume"
comparisons, Humphreys et
al. (2003a, p. 8) also have no basis for making the
following claims about "uniform" helium distributions
between the zircons and biotites of sample 6:
"So a possible explanation for sample 6 is that
diffusion into the surrounding materials (feldspar,
quartz), and leakage (along grain boundaries) was slow
enough (during the relatively short time t [i.e., t
= 6,000 years in the 'creation model']) to make the outflow
of helium from the biotite negligible. For that sample, the
temperature and diffusion coefficient were high enough for
helium to spread uniformly through both zircon and biotite
during that time."
In other words, Humphreys et al. assume that
surrounding quartz and feldspars essentially trapped the
helium in the biotites and zircons of sample 6 and allowed
the gas to uniformly distribute between the zircons and
surrounding biotites within 6,000 years. Because Humphreys
et al. have convinced themselves that the helium in
the biotites and zircons of sample 6 has nearly achieved
"equilibrium," they incorrectly believe that they are
justified in removing the sample from their "models."
Humphreys et al.
(2003a, p. 8) expand upon their fallacious arguments by
further concluding:
"Our measurements (see Appendix
B) showed that the helium concentration in the Jemez
[sic, gneiss] biotite at a depth of 750 meters was
small, only about 0.32 x 10‑9
cm3 (at STP) per microgram. Taking into account
the difference in density of biotite and zircon (3.2 g/cm
3 and 4.7 g/cm3), that corresponds to
almost exactly the same amount of helium per unit volume as
sample 6 contained. That suggests the zircon and biotite
were near equilibrium in sample 6, thus supporting our
hypothesis."
In these statements, Humphreys et al.
(2003a, p. 8) noticed similarities between the helium
concentrations of impure biotites (Appendix B in Humphreys et al.,
2003a, p. 19) from a gneiss collected at a depth of 750
meters and the zircons of sample 6 (Jemez Granodiorite[?],
4310 meters deep, revised helium data from Gentry et
al., 1982a). So, how can anyone argue that the helium
concentrations of the zircons and biotites in sample 6 are
essentially the same on the basis of comparing the amount
of helium in the zircons of the sample with the helium
concentration of impure biotites from a relatively shallow
gneiss? Again, Humphreys
et al. (2003a, p. 6) admit that mixing
measurements from different lithologies is inappropriate.
Even if the helium concentrations of the zircons at 4310
meters and the biotites at 750 meters happen to be similar,
couldn't the helium concentrations of the biotites at 4310
meters be even lower?
Although Humphreys et
al. (2003a, p. 13) eventually admit that that the
zircons and biotites in sample 5 may also have "uniform"
helium distributions, they never justify why sample 5
should be retained in their "models" and not removed along
with sample 6. Clearly, the helium in both samples 5 and 6
could have had the same origin. Again, they could both be
mostly analytical interference, contamination or extraneous
background helium. Until these issues are resolved,
Humphreys et al. simply have no justification for
treating sample 6 differently than 5.
Although the helium distribution between the biotites
and zircons of samples 5 and/or 6 may be uniform, Humphreys
et al. have not provided any evidence to
definitively support uniformity. Alternatively, numerous
fractures in surrounding minerals might have allowed the
helium to readily escape from the biotites of both samples
in the recent past, but not from the relatively impermeable
zircons. Clearly, for anyone to demonstrate uniform helium
distributions in samples 5 and 6, the helium concentrations
of the biotites and zircons of both samples should have
been analyzed when they were first recovered from the
subsurface in 1974.
Related Claims in Humphreys et al.
(2004)
In a related issue, Humphreys et al.
(2004, p. 9) attempt to respond to some criticisms from
old-Universe creationist Hugh Ross:
"Third, because the average volume of the biotite flakes
is hundreds of times greater than that of the zircons
(Humphreys et al., 2003a, section 6 [p. 7-10]), the amount
of helium in the biotites is on the same order of magnitude
as the amount of helium lost by the zircons. That rebuts a
specious uniformitarian conjecture (Ross, 2003) that there could have been
vast amounts (100,000 times greater than the already large
observed amounts) of non-radiogenic primordial helium in
the zircons 1.5 billion years ago."
Because Humphreys et al.’s arguments are
based on vague measurements of b, invalid isotropic
diffusion calculations on biotites which do not properly
consider the effects of multiple cleavage planes, a failure
to analyze for extraneous helium, a serious miscalculation
of the amount of helium in zircons from 750 meters depth
and many other illegitimate assumptions from their 2003a
document, they have no successful rebuttal to Ross and
their other critics.
FLAWED FOUNDATIONS OF HUMPHREYS ET
AL.'S MODELS
In summary, the relatively high helium concentrations in
the 750-meter zircons, the highly variable uranium and
thorium concentrations even in single zircons within the
Fenton Hill core (Gentry et
al., 1982b), and the inability of Humphreys et
al. to recognize different lithologies in the
subsurface of the Fenton Hill site (Sasada, 1989, p. 258; my Table 1)
indicate that the helium data in the Humphrey et al.
documents are too erroneous, anomalous and/or extraneous to
definitively fit into simplistic diffusion rate "models."
Until Humphreys et al. obtain adequate assistance
from the "next generation of analysts" and better define
the helium concentrations and Q/Q0 values
of their samples, their "modeling" efforts will not achieve
any scientific validity.
"MODELING" RESULTS: INCONSISTENT HELIUM
DIFFUSION "DATES"
Depending on which equations are used and what values
are entered into them, Humphreys et al.
(2003a) provide several different ways of generating
helium diffusion "dates." Although the equations in Humphreys et al.
(2003a) depend on many questionable or outright invalid
assumptions, the internal consistency of
these "dating" equations can be evaluated. That is, even if
the same values are entered into the various equations,
will they consistently derive "dates" that support the
"creation model"?
Table 4 summarizes various "creation model dates" that
Humphreys et al. have published in their 2003a and
2004 papers. The results in the 2003a paper are based on
lower-temperature extrapolations of higher temperature
helium diffusion data (Figure 8 in Humphreys et al.,
2003a, p. 11), whereas the 2004 data are supposedly
more directly based on lower temperature measurements of
diffusion coefficients (Figure 6 in Humphreys et al.,
2004, p. 7). Because Humphreys et al. consider
samples 1, 2002, and 2003 to be on a "defect line," they
derived no "dates" for them. Sample 2 was also considered
to lie on the "defect line" according to Humphreys et al.
(2003a), but the status of this sample changed in the
2004 article and a "date" was generated. Humphreys et
al. also recognize that sample 0 is not from Jemez
Granodiorite (see my Table 1), so no "date" was calculated
for it. As discussed above, Humphreys et al.
(2003a) believe that sample 6 is "a special case."
Therefore, no date was derived for this sample either.
Table 4. A comparison of helium diffusion "dates"
from Humphreys et al.
(2003a, p. 12) and Humphreys et al.
(2004, Table III, p. 8).
| No. |
Depth |
Dates in years from Humphreys et al.
(2003a) |
Errors (± years) for Humphreys et al.
(2003a) "dates" |
Dates in years from Humphreys et al.
(2004) |
| 0 |
Surface |
------- |
------- |
------- |
| 2002 |
750 |
------- |
------- |
------- |
| 1 |
960 |
------- |
------- |
------- |
| 2003 |
1490 |
------- |
------- |
------- |
| 2 |
2170 |
------- |
------- |
7,270 |
| 3 |
2900 |
10,389 |
+4,050; -2,490 |
2,400 |
| 4 |
3502 |
6,392 |
+2,110; -1,150 |
5,730 |
| 5 |
3930 |
4,747 |
------- |
~7,330 |
| 6 |
4310 |
------- |
------- |
------- |
| |
|
|
Average: |
"6000 ± 2000" |
Notice that some of the "dates" in Table 4 have
radically changed since 2003. In 2003, Humphreys et
al. predicted that sample 3 would have an "age"
somewhere between 7,899 and 14,439 years. Now, the "date"
is only 2,400 years, which is far outside the range of the
original 2003a prediction and too young even for YECs. The
2003a and 2004 "dates" for sample 5 are also significantly
different.
In Humphreys et al.
(2004, Table III, p. 8), the "dates" for samples 2-5
(i.e., 7270, 2400, 5730 and 7330 years) were
averaged. The average value of 5,681 years was then rounded
off to 6,000 years. Typically, standard deviations are
calculated with a "non-biased" equation, which uses degrees
of freedom (n-1) in the denominator rather than the
total number of samples (n) (Davis, 1986, p. 33; Keppel, 1991, p. 43-44, 58).
Furthermore, a standard deviation is often given as
two-sigma, which is large enough to include 95% of all
theoretical measurements. Such an approach would yield
6,000 ± 4,600 years for the results from Humphreys et al.
(2004). Instead of utilizing the traditional approach,
Humphreys et al.
(2004, Table III, p. 8) minimized their standard
deviation at ± 2,000 years by using the "biased"
equation (n instead of n-1 in the
denominator) and only reporting one-sigma (about 68% of the
measurements). This is an old statistical trick that some
individuals use to make their errors appear as small as
possible. Obviously, Humphreys
et al. (2004) would rather have their method
provide a most recent "creation date" of 2,000 BC instead
of 600 AD!
The Humphreys et
al. (2003a, 2004) "dates," which are listed in my
Table 4, were obtained from equations 14a-c and 17 in Humphreys et al.
(2003a). To derive their 2003a "dates," Humphreys et al.
(2003a, p. 9f) first inserted their
Q/Q0 values into equation 14a-b to
calculate x values for samples 1-5. Equation 14a-c
states:
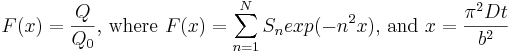
Where:
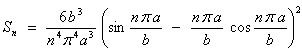
Other variables in equation 14a-c are defined above and
in Humphreys et al.
(2003a).
Humphreys et al.
(2003a, p. 10) list the resulting x values in
their Table 2. To calculate "dates" for samples 3-5,
Humphreys et al., (2003a, p. 11-12) entered x
values and dispersion coefficients derived from parameters
in 5b (p. 7) into equation 17. Equation 17 is simply a
rearrangement of equation 14c and states:
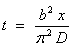
Because Humphreys et
al. (2003a, Figure 8, p. 11) believed that samples
1 and 2 were located on a "defect line," they argued that
equation 17 would only apply to samples 3-5. Recently,
however, Humphreys et
al. (2004) claim that sample 2 is actually part of
the intrinsic curve along with samples 3-5 rather than on a
"defect line." In Humphreys
et al. (2004, Table III, p. 8; also my Table 4),
new "dates" were obtained for samples 2-5 by entering the
x values from the 2003a paper and new 2004 diffusion
coefficients into equation 17.
Because their "uniformitarian model" (where t =
1.5 billion years) considers biotite to be a negligible
hindrance to helium flow, Humphreys et al.'s (2003a, p. 10-11) used equation 16
rather than 14a-b and 17 to calculate the diffusion
coefficients for this "model." Equation 16 states:
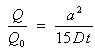
However, considering that Humphreys et al.'s
diffusion values were obtained on bare zircons under a
vacuum and that the helium concentrations and diffusion
results for their biotites are so poor and incomplete, why
couldn't equation 16 support the "creation model" just as
well or better than equations 14a-b and 17?
Because they failed to realize that their samples from
depths of 750 and 1490 meters actually came from a gneiss
and not the Jemez Granodiorite, Humphreys et al.
improperly mixed several measurements from different rock
types to produce "dates" for samples 3-5 in their 2003a
document and samples 2-5 in their 2004 article.
Specifically, the values for D and probably b
came from the gneiss, whereas their a and
Q/Q0 values are from Gentry et al. (1982a),
which include measurements on zircons from the Jemez
Granodiorite. As mentioned above, the mixing of these
parameters is inappropriate and would lead to even more
skepticism about their "dates."
Considering the inappropriate and simplistic assumptions
and the improper mixing of zircon measurements from
different rock types, there is no reason to believe that
any of the equations and associated results in Humphreys et al.
(2003a; 2004) and related YEC documents would
reasonably date the diffusion of helium in zircons.
Nevertheless, Humphreys et al.'s
(2003a) equations 14a-c, 16 and 17 should be simply
evaluated for internal consistency by calculating "dates"
for samples 2, 3, 4, and 5 using my Q/Q0
values. That is, will these equations produce similar
results? Are all of these dates really consistent with the
"creation model"?
In my calculations, laboratory-measured diffusion
coefficients were taken from Table III of Humphreys et al.
(2004, p. 8). Because no standard deviations are given
for the b values in Humphreys et al.
(2003a, p. 8) and because the values of the Jemez
Granodiorite biotites could be significantly different than
the measurements provided by Humphreys et al.,
alternative b values of 0.05 cm and 0.30 cm were
also used in the equations. This range of b values
provides some estimation of how variations in this
parameter could affect the "dating" results from these
equations.
Because Humphreys et
al. (2004, Table I, p. 3 and p. 5) admit that the
zircons from the 750 meter sample were not sorted by size,
values of a were allowed to vary at 0.0020, 0.0030
and 0.0040 cm. In my calculations with equation 14a-c, the
a values were paired with b values in such a
way as to obtain a maximum range of possible "dates." My
resulting "dates" are listed in Table 5 and compared with
"dates" from Humphreys et
al. (2004).
Table 5. Helium diffusion "dates" from equations
14a-c, 16 and 17 in Humphreys
et al. (2003a). My "dates" utilized my
Q/Q0 values. Because Gentry et al. (1982a)
could only approximate the helium measurement (Q)
for the zircons of sample 5, the Q/Q0
values and resulting "dates" for this sample are even less
certain than the results for the other samples. For my
equation 17 "dates," I used the x values from Table
2 in Humphreys et al.
(2003a, p. 10). None of my "dates" contain more than
two significant digits.
| No. |
a, cm |
b, cm |
My Q/Q0 |
My "Dates" in Years Using Eq. 14a-c and My
Q/Q0 Values |
My "Dates" in Years Using Eq. 16 |
My "Dates" in Years Using Eq. 17 |
Eq. 14a-c and 17 "Dates" in Years from Humphreys et al.
(2004) |
| |
|
|
|
|
|
|
|
| 2 |
0.002 |
0.05 |
0.088 |
9,700 |
8,800 |
1,800 |
|
| |
0.003 |
0.1 |
0.088 |
22,000 |
20,000 |
7,300 |
7,270 |
| |
0.004 |
0.3 |
0.088 |
39,000 |
35,000 |
65,000 |
|
| 3 |
0.002 |
0.05 |
0.068 |
2,400 |
2,300 |
600 |
|
| |
0.003 |
0.1 |
0.068 |
5,400 |
5,100 |
2,400 |
2,400 |
| |
0.004 |
0.3 |
0.068 |
9,600 |
9,100 |
22,000 |
|
| 4 |
0.002 |
0.05 |
0.0039 |
5,500 |
12,000 |
1,400 |
|
| |
0.003 |
0.1 |
0.0039 |
12,000 |
26,000 |
5,700 |
5,730 |
| |
0.004 |
0.3 |
0.0039 |
22,000 |
46,000 |
51,000 |
|
| 5 |
0.002 |
0.05 |
0.002 |
2,000 |
5,300 |
1,800 |
|
| |
0.003 |
0.1 |
0.002 |
4,600 |
12,000 |
7,300 |
~7,330 |
| |
0.004 |
0.3 |
0.002 |
8,200 |
21,000 |
66,000 |
|
| |
0.002 |
0.05 |
0.0005 |
5,200 |
21,000 |
1,800 |
|
| |
0.003 |
0.1 |
0.0005 |
12,000 |
48,000 |
7,300 |
|
| |
0.004 |
0.3 |
0.0005 |
21,000 |
85,000 |
66,000 |
|
| |
|
|
|
|
|
Average (years) |
12,000 |
24,000 |
20,000 |
6,000 |
| |
|
|
|
|
|
2-sigma Standard Dev. |
20,000 |
44,000 |
53,000 |
4,600 |
As shown in Table 5, the different "dating" equations
and parameters provide very inconsistent results, which are
often greater than 10,000 years old; that is, too old for
the YEC agenda. Considering the bogus assumptions that were
used to derive these equations, why should the results be
surprising and why should any of them be trusted?
Because no evidence exists for strong "defect lines" in
the data of Humphreys et
al. (2003a, 2004) (also see my Figure 1), the
consistency of equations 14a-c and 16 could be further
tested by deriving "dates" for samples 1, 2002, and 2003.
Additionally, because Humphreys et al.
(2003a) have no valid justification for excluding the
results of sample 6 from their "models" while retaining
those of sample 5, "dates" could also be calculated for
sample 6. Again, these "dates" probably have no time
significance, but they would test the consistency of
Humphreys et al.'s equations and supporting
assumptions.
Table 6 lists "dates" for all of the samples using my
Q/Q0 values. The Q/Q0
for the 2003 sample (1490 meters
depth) was estimated at 0.15; that is, 6.3 ncc STP/μg
from Humphreys et al.
(2004, Table I, p. 3) divided by my
Q0 of 41 ncc STP/μg. The
Q/Q0 values for samples 1, 5 and 6 in
Table 6 are maximum and minimum results that were derived
from the procedures in Appendix B.
Although these Q/Q0 values may be
unrealistically too high or too low, the resulting range of
"dates" will probably provide a strong sense of the
consistency between the Humphreys et al.
(2003a) equations and the "creation model." While the
diffusion coefficients for samples 2, 3, 4, and 5 were
taken from Table III in Humphreys et al.
(2004, p. 8), ranges of diffusion coefficients for the
other samples were estimated from Table II and Figure 6 of
Humphreys et al.
(2004, p. 6, 7). They varied from 1 x 10-14
cm2/sec to 1 x 10-15
cm2/sec for sample 6 (313°C) and as low as 1
x 10-17 cm2/sec to 1 x
10-18 cm2/sec (~100°C) for
samples 2002 and 1. For convenient comparisons, the results
in Table 5 from equations 14a-c and 16 are again listed in
Table 6.
The average of all of the "dates" in Table 6 and the
equation 17 "dates" from Table 5 is 85,000 ± 780,000
(two-sigma) years old. The "dates" range from -15,000 (due
to Q/Q0 > 1) to 3,100,000 years old.
Table 6. "Dates" for all of the Fenton Hill core
samples derived from equations in Humphreys et al.
(2003a, p. 9-11). Because Gentry et al. (1982a)
could only approximate the helium measurements (Q)
for the zircons of samples 5 and 6, the
Q/Q0 values and resulting "dates" for
these samples are even less certain than the results for
the other samples. The "dates" have been rounded off to no
more than two significant digits. Negative dates are due to
Q/Q0 values of greater than
one.
| No. |
a, cm |
b, cm |
Q/Q0 |
D, cm2/sec |
My "dates" (years) with eq. 14a-c |
My "dates" (years) with eq. 16 |
| |
|
|
|
|
|
|
| 2002 |
0.002 |
0.05 |
2.3 |
1.00E-17 |
-57 |
370 |
| |
0.003 |
0.1 |
2.3 |
1.00E-17 |
-210 |
830 |
| |
0.004 |
0.3 |
2.3 |
1.00E-17 |
-1,500 |
1,500 |
| |
0.002 |
0.05 |
2.3 |
1.00E-18 |
-570 |
3,700 |
| |
0.003 |
0.1 |
2.3 |
1.00E-18 |
-2,100 |
8,300 |
| |
0.004 |
0.3 |
2.3 |
1.00E-18 |
-15,000 |
15,000 |
| 1 |
0.002 |
0.05 |
0.21 |
1.00E-17 |
4,700 |
4,000 |
| |
0.003 |
0.1 |
0.21 |
1.00E-17 |
11,000 |
9,100 |
| |
0.004 |
0.3 |
0.21 |
1.00E-17 |
19,000 |
16,000 |
| |
0.002 |
0.05 |
0.21 |
1.00E-18 |
47,000 |
40,000 |
| |
0.003 |
0.1 |
0.21 |
1.00E-18 |
110,000 |
91,000 |
| |
0.004 |
0.3 |
0.21 |
1.00E-18 |
190,000 |
160,000 |
| |
0.002 |
0.05 |
0.011 |
1.00E-17 |
50,000 |
77,000 |
| |
0.003 |
0.1 |
0.011 |
1.00E-17 |
110,000 |
170,000 |
| |
0.004 |
0.3 |
0.011 |
1.00E-17 |
200,000 |
310,000 |
| |
0.002 |
0.05 |
0.011 |
1.00E-18 |
500,000 |
770,000 |
| |
0.003 |
0.1 |
0.011 |
1.00E-18 |
1,100,000 |
1,700,000 |
| |
0.004 |
0.3 |
0.011 |
1.00E-18 |
2,000,000 |
3,100,000 |
| 2003 |
0.002 |
0.05 |
0.15 |
1.00E-16 |
660 |
560 |
| |
0.003 |
0.1 |
0.15 |
1.00E-16 |
1,500 |
1,300 |
| |
0.004 |
0.3 |
0.15 |
1.00E-16 |
2,600 |
2,300 |
| |
0.002 |
0.05 |
0.15 |
1.00E-17 |
6,600 |
5,600 |
| |
0.003 |
0.1 |
0.15 |
1.00E-17 |
15,000 |
13,000 |
| |
0.004 |
0.3 |
0.15 |
1.00E-17 |
26,000 |
23,000 |
| 2 |
0.002 |
0.05 |
0.088 |
1.09E-17 |
9,700 |
8,800 |
| |
0.003 |
0.1 |
0.088 |
1.09E-17 |
22,000 |
20,000 |
| |
0.004 |
0.3 |
0.088 |
1.09E-17 |
39,000 |
35,000 |
| 3 |
0.002 |
0.05 |
0.068 |
5.49E-17 |
2,400 |
2,300 |
| |
0.003 |
0.1 |
0.068 |
5.49E-17 |
5,400 |
5,100 |
| |
0.004 |
0.3 |
0.068 |
5.49E-17 |
9,600 |
9,100 |
| 4 |
0.002 |
0.05 |
0.0039 |
1.87E-16 |
5,500 |
12,000 |
| |
0.003 |
0.1 |
0.0039 |
1.87E-16 |
12,000 |
26,000 |
| |
0.004 |
0.3 |
0.0039 |
1.87E-16 |
22,000 |
46,000 |
| 5 |
0.002 |
0.05 |
0.002 |
7.97E-16 |
2,000 |
5,300 |
| |
0.003 |
0.1 |
0.002 |
7.97E-16 |
4,600 |
12,000 |
| |
0.004 |
0.3 |
0.002 |
7.97E-16 |
8,200 |
21,000 |
| |
0.002 |
0.05 |
0.0005 |
7.97E-16 |
5,200 |
21,000 |
| |
0.003 |
0.1 |
0.0005 |
7.97E-16 |
12,000 |
48,000 |
| |
0.004 |
0.3 |
0.0005 |
7.97E-16 |
21,000 |
85,000 |
| 6 |
0.002 |
0.05 |
0.002 |
1.00E-14 |
160 |
420 |
| |
0.003 |
0.1 |
0.002 |
1.00E-14 |
370 |
950 |
| |
0.004 |
0.3 |
0.002 |
1.00E-14 |
650 |
1,700 |
| |
0.002 |
0.05 |
0.002 |
1.00E-15 |
1,600 |
4,200 |
| |
0.003 |
0.1 |
0.002 |
1.00E-15 |
3,700 |
9,500 |
| |
0.004 |
0.3 |
0.002 |
1.00E-15 |
6,500 |
17,000 |
| |
0.002 |
0.05 |
0.0002 |
1.00E-14 |
760 |
4,200 |
| |
0.003 |
0.1 |
0.0002 |
1.00E-14 |
1,700 |
9,400 |
| |
0.004 |
0.3 |
0.0002 |
1.00E-14 |
3,100 |
17,000 |
| |
0.002 |
0.05 |
0.0002 |
1.00E-15 |
7,600 |
42,000 |
| |
0.003 |
0.1 |
0.0002 |
1.00E-15 |
17,000 |
95,000 |
| |
0.004 |
0.3 |
0.0002 |
1.00E-15 |
31,000 |
170,000 |
|
|
|
|
Average |
92,000 |
140,000 |
|
|
|
|
2 sigma Std. Dev. |
650,000 |
990,000 |
MISCELLANEOUS ISSUES
Several other topics are briefly mentioned in Humphreys et al.
(2003a). Like their other discussions, Humphreys et
al. make a number of statements that are based on
questionable claims and outright errors.
Atmospheric Helium: YECs Lose Another
Argument
Humphreys et al.
(2003a, p. 2) briefly discuss the YEC atmospheric helium
argument. For years, Vardiman
(1990), Melvin Cook (see Cook,
1957) and other YECs have argued that the Earth's
atmosphere has too little helium to be billions of years
old. However, a review of Vardiman
(1990) and other YEC documents show that their
arguments are largely based on selective quoting of
outdated references from the 1960's and 1970's.
Dalrymple (1984, p. 112)
concisely challenges many of the YEC atmospheric helium
arguments. He shows that
YECs often omit critical details on various atmospheric
helium escape mechanisms, such photoionization. YECs also
tend to forget about the impacts of 20th century helium
pollution on any attempts to evaluate atmospheric escape
mechanisms.
Many YECs consider Vardiman
(1990) to be the authoritative YEC document on
atmospheric helium "dating." Even though Vardiman (1990) was written six
years after Dalrymple's report,
significant portions of this 1990 report simply repeat old
YEC arguments that had been refuted earlier by Dalrymple.
For example, carefully compare the statements in Dalrymple, 1984 (p. 112) with Vardiman (1990, p. 24-25).
More recent studies (such as
LieSvendsen and Rees, 1996;
Shizgal and Arkos, 1996)
provide additional information on helium escape mechanisms,
which further undermine YEC arguments on this issue.
Nevertheless, the final nail in the coffin of the YEC
atmospheric helium argument occurred when NASA satellite
images showed helium and other gases being
swept from the Earth's atmosphere into
deep space. One event occurred on September 24-25, 1998
after a solar coronal mass emission (see
Solar Wind Blows Some of the Earth's Atmosphere into
Space and
Solar Wind Squeezes Some of the Earth's Atmosphere into
Space).
In response to these recent observations, Humphreys et al.
(2003a, p. 2) only mention that YECs need to review the
new data. Clearly, the current scientific data indicate
that their helium arguments for a "young" Earth are as dead
as
their Moon Dust argument and the Paluxy "human"
footprints. Although they could always use their
imaginations and may be invoke a few miracles, Humphreys et al.
(2003a, p. 2) have decided to change tactics. They are
now speculating that there is too much helium in the
Earth's interior for our planet to be 4.6
billion years old.
Vardiman (1990, p. 28-29)
correctly states that YECs should study the atmospheric
residence times of heavier gases, like argon, which are
less likely to escape into space from the Earth’s
atmosphere. However, it is doubtful that such studies would
support their Genesis agenda. When compared with
36Ar, the Earth's atmosphere has excess
40Ar (Faure, 1986, p.
66), which is compatible with billions of years of
40K decay in terrestrial rocks (Dalrymple, 1984, p. 83; also see
Tolstikhin and Marty,
1998). In contrast, stellar atmospheres have more
36Ar than 40Ar (Krauskopf and Bird, 1995, p.
576), which is consistent with stellar evolution (Faure, 1998, p. 18).
Quoting 2 Peter 3:4 and Distorting
Reality AGAIN
YECs frequently quote 2 Peter
3:3-7 in their literature. Here is the King James Bible
Version:
"3:3 Knowing this first, that there shall come in
the last days scoffers, walking after their own lusts,
3:4 And saying, Where is the promise of his coming?
for since the fathers fell asleep, all things continue as
they were from the beginning of the creation. 3:5
For this they willingly are ignorant of, that by the word
of God the heavens were of old, and the earth standing out
of the water and in the water: 3:6 Whereby the world
that then was, being overflowed with water, perished:
3:7 But the heavens and the earth, which are now, by
the same word are kept in store, reserved unto fire against
the day of judgment and perdition of ungodly men."
YECs feel that this is a "prophecy" against
"uniformitarianism". Not surprisingly, Humphreys et al.
(2003a, p. 4) follow the YEC crowd and also cite 2
Peter 3:4,5-6 as part of their discussions. In reality, 2
Peter is probably a 2nd century
forgery written in response to non-Christian critics
calling the Christian's bluff on the "soon" Second Coming
of Christ (e.g.,
Revelation 1:3). The verses have
nothing to do with geology and because they're probably the
words of a forger, not even YECs should take them
seriously. In contrast to YECs that invoke creation myths,
"Flood geology" that has been thoroughly discredited since
the early 19th century, and false prophecies from the
Bible, scientists have often successfully explained
nature by only using natural explanations. So, contrary to
the statement in Humphreys
et al. (2003a, p. 4), the only "elephant in the
living room" is a pink YEC hallucination.
CONCLUSIONS
Despite enthusiastic endorsements by numerous YECs, the
"helium diffusion studies" in Humphreys et al.
(2003a,b; 2004) and Humphreys
(2003) are based on many flawed arguments, ad
hoc miracles, bad assumptions, untrustworthy equations,
and questionable data. For example, the relatively high
Q/Q0 values of some of the zircons, which
are important in deriving many of the YEC helium diffusion
"dates," may be due to extraneous helium or artifacts of
grossly underestimating the Q0 values of
uranium- and thorium-rich zircons.
Obviously, there are major and critical differences
between many YEC "researchers" and real scientists. Real
scientists pay attention to details in their research,
evaluate multiple natural hypotheses, see where their
research takes them, and ignore any pronouncements from the
Humanist Manifesto, the Bible, the Book of
Mormon, or the Koran. Because YECs already
believe that they have "The Answers" in their Bibles, they
tend to take an "ends justifies the means" approach to
"research," which often leads to careless actions,
including: taking unjustified shortcuts (such as, assuming
isotropic diffusion in biotites), using sloppy procedures
(for example, miscalculating Q for the 750-meter
zircons in Appendix C of Humphreys et al., 2003a),
and overlooking alternative natural explanations that
conflict with their agenda (as examples, extraneous helium
or exceptionally high uranium concentrations in many of
their zircons). After all, getting the "biblically correct
answers" and protecting their faith are paramount for most
YECs.
Because miracles, bad assumptions and questionable data
can be easily manipulated to produce any desired results,
it's not surprising that Humphreys et al. were able
to derive an "excellent creation model" with their "data."
It is unfortunate that expert geochemist Dr. Ken Farley was
not allowed to have a more prominent role in the efforts of
Humphreys et al. If he had, the results would have
been more reliable. On the other hand, it's doubtful that
the YECs would have obtained the results that their dogma
demands.
ACKNOWLEDGMENTS
Internet comments on Humphreys et al.
(2003a,b) and Humphreys
(2003) by "WeHappyFew", Dr. Joseph G. Meert, and Jack
DeBaun were exceptionally insightful. A number of
peer-reviewers and other individuals provided valuable
comments on various drafts of this manuscript, including:
Tom Baillieu, Tom Bridgman, John Brawley, Paul Heinrich,
Mark Isaak, Mark D. Kluge, Ted Lawry and
Frank Lovell. I thank Mike Hopkins for his hard work in proofreading and
posting this essay on the Internet.
REFERENCES (including Internet links,
when available)
Bailey, S.W.,
1984, "Crystal Chemistry of the True Micas," Reviews
in Mineralogy, v. 13, p. 13-60.
Baxter, E.F.,
2003, "Quantification of the Factors Controlling the
Presence of Excess 40Ar or 4He,"
Earth Planet. Sci. Lett., v. 216, p.
619-634.
Cook, M., 1957,
"Where is the Earth's Radiogenic Helium?",
Nature, n. 4552, January 26, p. 213.
Dalrymple, G. B., 1984, "How Old
is the Earth?: A Reply to `Scientific' Creationism,"
in Proceedings of the 63rd Annual Meeting of the
Pacific Division, American Association for the Advancement
of Science, v. 1, pt. 3, Frank Awbrey and William
Thwaites (Eds).
Davis, J.C.,
1986, Statistics and Data Analysis in Geology,
2nd ed., John Wiley & Sons, New York.
Delsemme,
A., 1998, Our Cosmic Origins: From the Big Bang to
the Emergence of Life and Intelligence, Cambridge
University Press, Cambridge, United Kingdom.
Farley, K.A., 2002,
"(U-Th)/He Dating: Techniques, Calibrations, and Applications,"
Rev. Min. Geochem., v. 47, p. 819-844.
Farley,
K.A., R.A. Wolf, and L.T. Silver, 1996, "The Effects of
Long Alpha-stopping Distances on (U-Th)/He Ages,"
Geochim. et Cosmo. Acta., v. 60, n. 21, p.
4223-4229.
Faure, G., 1986,
Principles of Isotope Geology, 2nd ed., John
Wiley & Sons, New York.
Faure, G., 1998,
Principles and Applications of Geochemistry,
2nd ed., Prentice Hall, Upper Saddle River, NJ.
Gentry, R.V., G.L. Gush, and
E.R. McBay, 1982a, "Differential Helium Retention in
Zircons: Implications for Nuclear Waste Cortainment,"
Geophys. Res. Letters, v. 9, n. 10, p.
1129-1130.
http://www.halos.com/reports/grl-1982-helium-in-zircons.pdf
Gentry, R.V., T.J. Sworski, H.S.
McKown, D.H. Smith, R.E. Eby, and W.H. Christie, 1982b,
"Differential Lead Retention in Zircons: Implications for
Nuclear Waste Containment," Science, v. 216,
April 16, p. 296-298.
http://www.halos.com/reports/science-1982-lead-in-zircons.pdf
Gentry, R.V.,
1984, "Lead Retention in Zircons: Reply,"
Science, v. 223, n. 4658, p. 835.
Girifalco, L.A., 1964,
Atomic Migration in Crystals, Blaisdell Pub.
Co., New York.
Goff,
F. and J. N. Gardner, 1994, "Evolution of a Mineralized
Geothermal System, Valles Caldera, New Mexico,"
Economic Geology, v. 89, p. 1803-1832.
Hanes, J.A.,
1991, "K-Ar and 40Ar/39Ar Geochronology: Methods and
Applications", in Applications of Radiogenic Isotope
Systems to Problems in Geology, L. Heaman and J.N.
Ludden (eds.), Short Course Handbook, v. 19, p. 27-57.
Harrison, T. M.; P. Morgan and
D. D. Blackwell, 1986, "Constraints on the Age of Heating
at the Fenton Hill Site, Valles Caldera, New Mexico,"
J. Geophys. Res. v. 91, n. B2, p.
1899-1908.
Humphreys, D.R.; S.A. Austin;
J.R. Baumgardner and A.A. Snelling, 2003a, "Helium
Diffusion Rates Support Accelerated Nuclear Decay,"
Proceedings of the Fifth International Conference on
Creationism, R. Ivey (ed.), Creation Science
Fellowship, Pittsburgh, PA.
http://globalflood.org/papers/2003ICChelium.html
Humphreys, D.R.; S.A. Austin;
J.R. Baumgardner and A.A. Snelling, 2003b, "Precambrian
Zircons Yield a Helium Diffusion Age of 6,000 Years,"
American Geophysical Union Fall Conference, Abstract
V32C-1047.
http://www.icr.org/research/AGUHeliumPoster_Humphreys.pdf
Humphreys, D.R., 2003, "New RATE
Data Support Young World," Impact, n. 366,
Institute for Creation Research.
http://www.icr.org/index.php?module=articles&action=view&ID=114
Humphreys, D.R., S.A Austin,
J.R. Baumgardner, and A.A. Snelling, 2004, "Helium
Diffusion Age of 6,000 Years Supports Accelerated Nuclear
Decay," Creation Research Society Quarterly,
v. 41, n. 1, June, p. 1-16.
http://www.creationresearch.org/crsq/articles/41/41_1/Helium.htm
Hyndman,
D.W., 1985, Petrology of Igneous and Metamorphic
Rocks, McGraw-Hill, New York.
Keppel, G.,
1991, Design and Analysis: A Researcher's
Handbook, 3rd ed., Prentice Hall, Engelwood Cliffs,
NJ.
Klein, C., 2002,
Mineral Science, 22nd ed., John Wiley &
Sons, New York.
Krauskopf, K.B. and D.K. Bird,
1995, Introduction to Geochemistry, 3rd ed.,
WCB McGraw-Hill, Boston, MA.
Langmuir, D.,
1996, Aqueous Environmental Geochemistry,
Prentice-Hall, Upper Saddle River, NJ.
Lee, J.K.W.,
I.S. Williams, and D.J. Ellis, 1997, "Pb, U and Th
Diffusion in Natural Zircon," Nature, v. 390,
p. 159-162.
LieSvendsen, O. and M.H.
Rees, 1996, "Helium Escape from the Terrestrial Atmosphere:
The Ion Outflow Mechanism," J. of Geophys. Res. -
Space Phys., v. 101, n. A2, p. 2435-2443.
Lippolt, H.J. and E. Weigel,
1988, "4He Diffusion in
40Ar-retentive Minerals," Geochim. et
Cosmo. Acta, v. 52, p. 1449-1458.
Ludwig,
K.R., R.E. Zartman, and S.S. Goldich, 1984, "Lead Retention
in Zircons," Science, v. 223, n. 4638, p.
835.
Magomedov, Sh. A., 1970,
"Migration of Radiogenic Products in Zircon,"
Geokhimiya, v. 2, p. 263-267 (in Russian).
English abstract: Geochemistry International,
v. 7, n. 1, p. 203.
McDougall, I. and T. M.
Harrison, 1999, Geochronology and Thermochronology by
the 40Ar/39Ar Method, Oxford
University Press, New York.
Nicolaysen, L.O., 1957, "Solid
Diffusion in Radioactive Minerals and the Measurement of
Absolute Age," Geochim. Cosmochim. Acta, v.
11, p. 41-59.
Perkins, D. and K.R. Henke,
2004, Minerals in Thin Section, Pearson
Prentice-Hall, Upper Saddle River, NJ 07458.
Reiners, P.W., K.A. Farley, and
H.J. Hickes, 2002, "He Diffusion and (U-Th)/He
Thermochronometry of Zircon: Initial Results from Fish
Canyon Tuff and Gold Butte," Tectonophysics,
v. 349, p. 297-308.
Ross, H., 2003,
"Reasons to Believe" radio broadcast, Sept. 18, 6-8pm
Pacific US Time. http://www.icr.org/headlines/rate-hughross.html
Sasada, M.,
1989, "Fluid Inclusion Evidence for Recent Temperature
Increases at Fenton Hill Hot Dry Rock Test Site West of the
Valles Caldera, New Mexico, U.S.A., J. Volc. and
Geotherm. Res., v. 36, p. 257-266.
Shizgal, B.D. and G.G. Arkos,
1996, "Nonthermal Escape of the Atmospheres of Venus,
Earth, and Mars," Rev. of Geophy. v. 34, n. 4,
p. 483-505.
Smith, S. P. and B. M. Kennedy,
1985, "Noble Gas Evidence for Two Fluids in the Baca
(Valles Caldera) Geothermal Reservoir," Geochimica et
Cosmochimica Acta, v. 49, p. 893-902.
Snelling, A.A. and J.
Woodmorappe, 1998, “The Cooling of Thick Igneous
Bodies on a Young Earth,” Proceedings of the
Fourth International Conference on Creationism, Aug.
3-8, Pittsburgh, PA, USA, Technical Symposium Sessions, R.
E. Walsh (ed.), Creation Science Fellowship, Inc., 705
Washington Dr., Pittsburgh, PA, USA 15229.
Tagami,
T., K.A. Farley, and D.F. Stockli, 2003, "(U-Th)/He
Geochronology of Single Zircon Grains of Known Tertiary
Eruption Age," Earth Planet. Sci. Letters, v.
207, p. 57-67.
Tolstikhin, I.N. and B.
Marty, 1998, "The Evolution of Terrestrial Volatiles: A
View from Helium, Neon, Argon and Nitrogen Isotope
Modelling," Chem. Geol., v. 147, p. 27-52.
Vardiman,
L., 1990, The Age of the Earth's Atmosphere: A Study
of the Helium Flux through the Atmosphere, Institute
for Creation Research, El Cajon, CA.
Vardiman, L., A.A. Snelling and
E.F. Chaffin (eds.), 2000, Radioisotopes and the Age
of the Earth, Institute for Creation Research, El
Cajon, CA and Creation Research Society, St. Joseph,
Mo.
Winkler,
H.G.F., 1979, Petrogenesis of Metamorphic
Rocks, 5th ed., Springer-Verlag, New York.
Zartman, R.
E., 1979, Uranium, thorium, and lead isotopic
composition of biotite granodiorite (Sample 9527-2b) from
LASL Drill Hole GT-2, Los Alamos Scientific
Laboratory Report LA-7923-MS.
APPENDIX A: CALCULATION OF
Q/Q0 VALUES USING ASSUMPTIONS IN GENTRY
ET AL. (1982a)
Q refers to the measured quantity of helium
(presumably only radiogenic 4He) in a mineral.
From its crystallization to the present,
Q0 is the maximum amount of radiogenic
helium (4He) that could accumulate in a mineral
from the radioactive decay of its uranium and thorium (Humphreys et al.,
2003a, p. 3). Q0 assumes that no
diffusion ("leakage") has occurred except for "alpha
ejection." Q/Q0 would then represent the
fraction of radiogenic 4He (that is, presumably
without any extraneous component) remaining in the sample
since its crystallization.
By making several very questionable
assumptions, Gentry et
al. (1982a, p. 1129) estimated the
Q/Q0 values of the zircons in their
samples. Gentry et al.
(1982a, p. 1129) state their assumptions in the
following paragraph:
"For the other zircons from the granite [sic,
granodiorite] and gneiss cores [samples 1-6], we made the
assumption that the radiogenic Pb concentration in zircons
from all depths was, on the average, the same as that
measured (Zartman, 1979) at 2900
m, i.e., ~80 ppm with
206Pb/207Pb and
206Pb/208Pb ratios of ten (Gentry
et al., ...[1982b]; Zartman,
1979). Since every U and Th derived atom of
206Pb, 207Pb, and 208Pb
represents 8, 7 and 6 alpha-decays respectively, this means
there should be ~7.7 atoms of He generated for every Pb
atom in these zircons."
First of all, they assumed that the radiogenic lead
concentrations (total 206Pb, 207Pb,
and 208Pb) of the zircons from each of the six
samples averaged 80 parts per million (ppm). Of course,
this assumption may not be accurate. Nevertheless:
80 ppm = 80 micrograms radiogenic Pb/gram zircon =
0.00008 g radiogenic Pb/g zircon
Although the overall atomic mass of Pb (207.2 amu)
includes non-radiogenic 204Pb, the atomic mass
of radiogenic Pb is close to 207.2 amu. Therefore:
0.00008 g/g divided by 207.2 g Pb/mole Pb = 3.9 x
10-7 moles radiogenic Pb/g zircon
The concentrations of the various radiogenic lead
isotopes are then represented by the following
equation:
206Pb + 207Pb + 208Pb =
3.9 x 10-7 moles total radiogenic Pb/gram
zircon
Given:
206Pb/207Pb = 10. That is:
207Pb = 206Pb/10. Gentry et
al.'s (1982a) assumption is
reasonable here. Actual values from Gentry et al. (1982b, p.
296) are about 9.6 to 11.2.
206Pb/208Pb = 10. That is:
208Pb = 206Pb/10. This assumption by
Gentry et al. (1982a)
is more questionable. Gentry
et al. (1982b, p. 296) has actual values as low
as 3.1 and as high as 14.
Combining these equations and using some algebra:
206Pb + 206Pb/10 +
206Pb/10 = 3.9 x 10-7 moles/g
Multiplying everything by 10:
10(206Pb) + 206Pb +
206Pb = 3.9 x 10-6 moles/g
12 (206Pb) = 3.9 x 10-6
206Pb = 3.25 x 10-7 mole/g
Then: 207Pb = 208Pb = 3.25 x
10-8 mole/g
Gentry et al.
(1982a, p. 1129) state:
"During the decay of uranium and thorium, every
206Pb, 207Pb, and 208Pb
atom has 8, 7, and 6 alpha-decays, respectively."
Therefore:
Total radiogenic 4He produced with the
radiogenic Pb:
Total radiogenic 4He = 8(206Pb in
moles) + 7(207Pb in moles) + 6(208Pb
in moles)
Total radiogenic He = 8(3.25 x 10-7) + 7(3.25
x 10-8) + 6(3.25 x 10-8) = 2.60 x
10-6 + 2.275 x 10-7 + 1.95 x
10-7 = 3.02 x 10-6 moles/g
There are 109 nanomoles in one mole.
Total radiogenic He = 3.02 x 10-6 moles/g x
109 nanomoles/mole = 3020 nanomoles He/gram of
zircon
Converting to Humphreys et al.'s scale of cubic
centimeters (Standard Temperature and Presssure [STP]) of
radiogenic He/microgram zircon requires the following
steps:
Gas laws state that at standard atmospheric temperature
and pressure (STP) 1 mole of every gas has a volume of 22.4
liters:
22.4 liters = 22,400 milliliters (ml)
1.0 ml = 1.0 cubic centimeter (cc)
Therefore: 22.4 liters = 22,400 cc
Total radiogenic He = 3020 x 10-9 moles/g x
22,400 cc STP/mole = 6.8 x10-2 cc STP/g
There are 106 micrograms in one gram.
Therefore:
6.8 x 10-2 cc STP/g divided by 106
micrograms/g = 6.8 x 10-8 cc STP/microgram
Assuming that up to 40% of the radiogenic helium is lost
by alpha ejection as Gentry
et al. (1982a, p. 1129-1130) argue, then:
60% of 6.8 x 10-8 cc STP/microgram = 41 x
10-9 cc STP radiogenic He/microgram zircon =
Q0
According to Humphreys
et al. (2004, p. 9), Gentry somehow obtained a
Q0 value for his zircons of approximately
15 x 10-9 cc STP/microgram. How Gentry exactly
derived this value is not discussed in Gentry et al.
(1982a) or Gentry et al.
(1982b). Nevertheless, my Q0 based on
Gentry et al.'s (1982a)
assumptions is considerably higher.
Using the measured helium concentrations (Q
values) listed in Humphreys
et al. (2003a, p. 3), I obtain my
Q/Q0 values. They are listed in Table A.
The use of alpha ejection percentages below 40% would lower
my Q/Q0 values even further.
Table A: Estimated Q/Q0 values
for zircons in the Fenton Hill, New Mexico well cores using
assumptions from Gentry et
al. (1982a, p. 1130) and revised data from Humphreys et al.
(2003a, p. 3). For my Q/Q0 values, an
alpha ejection value of 40% was assumed. The use of lower
alpha ejection percentages would increase my
Q0 and lower my Q/Q0
values even further.
| No. |
Depth (m) |
Revised He concentrations (Q) in Humphreys
et al. (cc STP/microgram) |
Humphreys et al.'s Q/Q0
±30% (using Q0 ~ 15 x
10-9 cc STP/microgram) |
My calculated Q/Q0 |
| 1 |
960 |
8.6 x 10-9 |
0.58 |
0.21 |
| 2 |
2170 |
3.6 x 10-9 |
0.27 |
0.088 |
| 3 |
2900 |
2.8 x 10-9 |
0.17 |
0.068 |
| 4 |
3502 |
1.6 x 10-10 |
0.012 |
0.0039 |
| 5 |
3930 |
~2 x 10-11 |
~0.001 |
~0.0005 |
| 6 |
4310 |
~2 x 10-11 |
~0.001 |
~0.0005 |
APPENDIX B: CALCULATION OF
Q0 AND ESTIMATED Q/Q0
VALUES FOR INDIVIDUAL ZIRCONS FROM SAMPLES 1, 5 AND 6 USING
CHEMICAL DATA FROM GENTRY ET AL. (1982b)
Gentry et al.
(1982b) list chemical data for individual zircons taken
from depths of 960, 3930 and 4310 meters in the Fenton Hill
cores (samples 1, 5 and 6 in Gentry et al., 1982a).
These data allow the Q0 values for the
three samples to be better defined than simply utilizing
the generic values that were calculated for samples 1-6 by
Gentry et al. (15 ncc STP/μg, Humphreys et
al., 2004, p. 9) or in Appendix A of this report (41
ncc STP/μg). The new Q0 values may
then be used to roughly estimate the range of possible
Q/Q0 values for the three samples.
Table B1 shows the range of uranium and thorium
concentrations for seven different zircons from samples 1,
5 and 6 (Gentry et al.,
1982b, p. 296). The letters associated with the sample
numbers in Table B1 represent different zircon specimens
that were analyzed from each depth by Gentry et al.
(1982b).
Table B1: Uranium and thorium concentrations on
seven zircons from the Fenton Hill well cores (Gentry et al., 1982b).
The analyses for the different zircons in Gentry et al. (1982b)
are numbered according to the scheme in Table 1 of this
report and letters are used to distinguish different
zircons from the same depth.
| Zircon ID |
Depth (m) |
U (parts per million) |
Th (parts per million) |
| |
|
|
|
| 1A |
960 |
240 - 5300 |
800 – 2000 |
| 1B |
960 |
465 - 1130 |
220 – 750 |
| 1C |
960 |
1250 - 3300 |
100 – 275 |
| 5A |
3930 |
83 - 220 |
63 – 120 |
| 5B |
3930 |
90 - 110 |
60 – 90 |
| 6A |
4310 |
110 - 550 |
63 – 175 |
| 6B |
4310 |
125 - 210 |
40 – 85 |
Typically, Gentry et
al. (1982b) performed four pairs of uranium and
thorium analyzes on each zircon. Gentry et al. (1982b)
noticed that the uranium and thorium concentrations varied
considerably even at different locations on the same zircon
grain. When calculating the concentrations, Gentry et al. (1982b)
assumed that the zircons were pure ZrSiO4.
Although zircons typically contain 1-4% hafnium (Klein, 2002, p. 498), this assumption
is probably reasonable.
The calculations in this appendix were performed on a
Microsoft ExcelTM spreadsheet. The calculations
assume no uranium or thorium addition or loss in the
zircons over time. To obtain a maximum possible range of
helium Q0 values for each zircon in Table
B1, the calculations paired up the highest uranium
concentration for each zircon with its highest
concentration of thorium and the lowest uranium
concentration with the lowest thorium value.
Table B2 shows the current maximum and minimum uranium
and thorium concentrations for each zircon from the
Precambrian gneiss at a depth of 960 meters (sample 1).
Parts-per-million (ppm) values are the same as
micrograms/gram. The micrograms/gram concentrations may be
divided by 1 x 106 micrograms/gram to convert
them into grams of element/gram of zircon. Concentrations
in moles element/gram zircon are obtained by dividing the
grams/gram concentrations by the atomic weights of uranium
and thorium (238.03 and 232.038 g/mole, respectively). Now,
99.2743% of modern natural uranium is 238U and
only 0.7200% is 235U (Faure, 1998, p. 284). These
percentages are used to determine the concentrations in
moles/g of each uranium isotope as shown in Table B2. Next,
the moles/g of 238U, 235U, and
232Th are multiplied by Avogadro's number (6.022
x 1023 atoms/mole) to obtain the total number of
atoms (N) of each isotope in every gram of
zircon.
Table B2: Concentrations of uranium and thorium in
three zircons (A, B and C) from a depth of 960 meters
(sample 1).
| Zircon |
Element |
Current conc., ppm |
mole/g |
mole/g 238U |
mole/g, 235U |
N, atoms/g |
| |
|
|
|
|
|
|
| 1A |
U minimum |
240 |
1.01E-06 |
1.00E-06 |
|
6.03E+17 |
| |
|
|
|
|
7.26E-09 |
4.37E+15 |
| 1A |
Th minimum |
800 |
3.45E-06 |
|
|
2.08E+18 |
| |
|
|
|
|
|
|
| 1A |
U maximum |
5300 |
2.23E-05 |
2.21E-05 |
|
1.33E+19 |
| |
|
|
|
|
1.60E-07 |
9.66E+16 |
| 1A |
Th maximum |
2000 |
8.62E-06 |
|
|
5.19E+18 |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 1B |
U minimum |
465 |
1.95E-06 |
1.94E-06 |
|
1.17E+18 |
| |
|
|
|
|
1.41E-08 |
8.47E+15 |
| 1B |
Th minimum |
220 |
9.48E-07 |
|
|
5.71E+17 |
| |
|
|
|
|
|
|
| 1B |
U maximum |
1130 |
4.75E-06 |
4.71E-06 |
|
2.84E+18 |
| |
|
|
|
|
3.42E-08 |
2.06E+16 |
| 1B |
Th maximum |
750 |
3.23E-06 |
|
|
1.95E+18 |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 1C |
U minimum |
1250 |
5.25E-06 |
5.21E-06 |
|
3.14E+18 |
| |
|
|
|
|
3.78E-08 |
2.28E+16 |
| 1C |
Th minimum |
100 |
4.31E-07 |
|
|
2.60E+17 |
| |
|
|
|
|
|
|
| 1C |
U maximum |
3300 |
1.39E-05 |
1.38E-05 |
|
8.29E+18 |
| |
|
|
|
|
9.98E-08 |
6.01E+16 |
| 1C |
Th maximum |
275 |
1.19E-06 |
|
|
7.14E+17 |
According to Appendix A in Humphreys et al.
(2003a), the zircons at 750 meters depth are 1.4393
billion years old. Zartman
(1979) found the zircons at 2903.8 meters depth to be
1.500 billion years old. I'll assume that the zircons at
960 meters depth are about 1.44 billion years old. For the
samples at 3930 and 4310 meters, I'll agree with Humphreys et al.
(2003a, p. 11) and assume an age of 1.5 billion
years.
The following equations and data from Faure (1998, p. 281-284) are used to
calculate the number of moles of radiogenic lead and helium
(Q0) produced from the decay of
238U, 235U and 232Th over
1.44 to 1.5 billion years. In reality, volcanism, tectonism
and metamorphism could have partially or entirely degassed
the zircons of helium long ago. At least some of the
current helium concentration could also consist of
extraneous 4He and 3He.
D* =
N(eλt -1)
D* = number of radiogenic Pb atoms
N = number of uranium and thorium atoms
currently present in the sample.
λ = decay constants:
λ for 238U = 1.55125 x
10-10 1/year
λ for 235U = 9.8485 x 10-10
1/year
λ for 232Th = 4.9475 x
10-11 1/year
t = age of the sample
The number of daughter atoms (a D*
value for 206Pb, 207Pb, and
208Pb) can now be calculated, as shown in Table
B3. For every 206Pb atom produced by the decay
of 238U, 8 4He atoms form. The
formation of a 207Pb atom results in the
formation of 7 4He atoms and 6 4He
atoms are associated with every 208Pb atom (Gentry et al., 1982a, p.
1129). Table B3 lists the number of radiogenic helium atoms
that would be produced by 1.44 billion years worth of
radioactive decay of 232Th, 235U, and
238U.
Table B3: Further calculations for zircons from
960 meters deep.
| Zircon |
Element |
Current conc., ppm |
Parent/daughter
isotopes |
D*(Pb) atoms/g |
He atoms/g |
| |
|
|
|
|
|
| 1A |
U min |
240 |
U-238/Pb-206 |
1.51E+17 |
1.21E+18 |
| |
|
|
U-235/Pb-207 |
1.37E+16 |
9.58E+16 |
| 1A |
Th min |
800 |
Th-232/Pb-208 |
1.53E+17 |
9.20E+17 |
| |
|
|
|
|
|
| 1A |
U max |
5300 |
U-238/Pb-206 |
3.33E+18 |
2.67E+19 |
| |
|
|
U-235/Pb-207 |
3.02E+17 |
2.12E+18 |
| 1A |
Th max |
2000 |
Th-232/Pb-208 |
3.83E+17 |
2.30E+18 |
| |
|
|
|
|
|
| |
|
|
|
|
|
| 1B |
U min |
465 |
U-238/Pb-206 |
2.92E+17 |
2.34E+18 |
| |
|
|
U-235/Pb-207 |
2.65E+16 |
1.86E+17 |
| 1B |
Th min |
220 |
Th-232/Pb-208 |
4.22E+16 |
2.53E+17 |
| |
|
|
|
|
|
| 1B |
U max |
1130 |
U-238/Pb-206 |
7.10E+17 |
5.68E+18 |
| |
|
|
U-235/Pb-207 |
6.44E+16 |
4.51E+17 |
| 1B |
Th max |
750 |
Th-232/Pb-208 |
1.44E+17 |
8.63E+17 |
| |
|
|
|
|
|
| |
|
|
|
|
|
| 1C |
U min |
1250 |
U-238/Pb-206 |
7.86E+17 |
6.29E+18 |
| |
|
|
U-235/Pb-207 |
7.13E+16 |
4.99E+17 |
| 1C |
Th min |
100 |
Th-232/Pb-208 |
1.92E+16 |
1.15E+17 |
| |
|
|
|
|
|
| 1C |
U max |
3300 |
U-238/Pb-206 |
2.07E+18 |
1.66E+19 |
| |
|
|
U-235/Pb-207 |
1.88E+17 |
1.32E+18 |
| 1C |
Th max |
275 |
Th-232/Pb-208 |
5.27E+16 |
3.16E+17 |
Avogadro's number is used to convert the number of
radiogenic helium atoms into moles (Table B4). For each
minimum and maximum zircon calculation, the helium
concentrations in moles associated with the decay of
238U, 235U, and 232Th are
summed (Table B4). Following the usage in Gentry et al. (1982a),
Humphreys et al.
(2003a), and Appendix A in
this document, the moles of radiogenic helium are then
converted into cubic centimeters of helium per microgram of
zircon at standard temperature and pressure (STP) (Table
B4).
Table B4: Further calculations for zircons from
960 meters deep.
| Zircon |
Element |
Current conc., ppm |
Isotope |
mole He/g |
Total mole He/g |
He cc STP/g |
He cc STP/μg |
| |
|
|
|
|
|
|
|
| 1A |
U min |
240 |
U-238 |
2.00E-06 |
3.69E-06 |
8.27E-02 |
8.27E-08 |
| |
|
|
U-235 |
1.59E-07 |
|
|
|
| 1A |
Th min |
800 |
Th-232 |
1.53E-06 |
|
|
|
| |
|
|
|
|
|
|
|
| 1A |
U max |
5300 |
U-238 |
4.43E-05 |
5.16E-05 |
1.16 |
1.16E-06 |
| |
|
|
U-235 |
3.51E-06 |
|
|
|
| 1A |
Th max |
2000 |
Th-232 |
3.82E-06 |
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 1B |
U min |
465 |
U-238 |
3.88E-06 |
4.61E-06 |
0.103 |
1.03E-07 |
| |
|
|
U-235 |
3.08E-07 |
|
|
|
| 1B |
Th min |
220 |
Th-232 |
4.20E-07 |
|
|
|
| |
|
|
|
|
|
|
|
| 1B |
U max |
1130 |
U-238 |
9.44E-06 |
1.16E-05 |
0.260 |
2.60E-07 |
| |
|
|
U-235 |
7.49E-07 |
|
|
|
| 1B |
Th max |
750 |
Th-232 |
1.43E-06 |
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 1C |
U min |
1250 |
U-238 |
1.04E-05 |
1.15E-05 |
0.257 |
2.57E-07 |
| |
|
|
U-235 |
8.28E-07 |
|
|
|
| 1C |
Th min |
100 |
Th-232 |
1.91E-07 |
|
|
|
| |
|
|
|
|
|
|
|
| 1C |
U max |
3300 |
U-238 |
2.76E-05 |
3.03E-05 |
0.678 |
6.78E-07 |
| |
|
|
U-235 |
2.19E-06 |
|
|
|
| 1C |
Th max |
275 |
Th-232 |
5.25E-07 |
|
|
|
As discussed in the main text, the alpha ejections of
these zircons were most likely 30-50%. To derive a maximum
range of Q0 values for each zircon, the
calculations using the maximum uranium and thorium
concentrations were assigned an alpha ejection value of
only 30% and the calculations with the minimum values were
given a value of 50%. The resulting Q0
values are shown in Table B5. To obtain highly accurate
Q/Q0 values for every zircon, the helium
concentration (Q) of each zircon must be known.
Unfortunately, this information is not available. Because
the uranium, thorium and Q0 values of the
individual zircons are highly variable (Tables B1 and B5),
large variations in the Q values are also expected
for the different zircons. Until the critical Q data
become available, only educated guesses can be made about
the possible ranges of Q/Q0 values for
samples 1, 5 and 6. An individual might estimate the range
of possible Q/Q0 values for each sample
by dividing the maximum and minimum Q0
values for each zircon into Humphreys et al.'s
revised Q values for each sample (from my Table 1).
For example, as shown in Table B6, the overall Q of
8.60 ncc STP/μg zircon may divided by the various
Q0 values for zircons 1A-1C to obtain a
series of Q/Q0 values for sample 1. They
range from 0.011 to 0.21. Probably fortuitously, the
maximum Q/Q0 value of 0.21 is identical
to the calculations for sample 1 in Appendix A. The maximum
and minimum Q/Q0 values for the zircons
at depths of 3930 and 4310 meters were calculated in the
same way and are shown as approximations in Table 3.
Although the ranges in Table 3 provide a rough idea of
how the Q/Q0 values could possibly vary
for the different samples, a more typical approximation for
the zircons might be obtained by dividing the sample's
overall Q value from Table 1 by the
average Q0 value for the
group. For sample 1, the average of the
Q0 values in Table B5 is 281 ncc
STP/μg. Therefore, the best currently available estimate
of Q/Q0 for sample 1 is probably 8.6 ncc
STP/μg divided by 281 ncc STP/μg or 0.031.
Unfortunately, the data in Gentry et al. (1982a,b)
and Humphreys et al.
(2003a; 2004) are too inadequate and poorly defined to
obtain any definitive Q/Q0 values for the
Fenton Hill core samples. Without suitable data, the
"modeling" efforts and helium diffusion "dates" in Humphreys et al.
(2003a,b; 2004) and Humphreys
(2003) are unreliable and even deceptive.
Table B5: Calculation of Q0
values for three zircons from 960 meters.
| Zircon |
Element |
Current conc., ppm |
Total He, cc STP/μg |
Q0 in ncc STP/μg after 30 -50%
boundary loss effects |
| |
|
|
|
|
| 1A |
U min |
240 |
8.27E-08 |
41.3 |
| |
|
|
|
|
| 1A |
Th min |
800 |
|
|
| |
|
|
|
|
| 1A |
U max |
5300 |
1.16E-06 |
809 |
| |
|
|
|
|
| 1A |
Th max |
2000 |
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| 1B |
U min |
465 |
1.03E-07 |
51.7 |
| |
|
|
|
|
| 1B |
Th min |
220 |
|
|
| |
|
|
|
|
| 1B |
U max |
1130 |
2.60E-07 |
182 |
| |
|
|
|
|
| 1B |
Th max |
750 |
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| 1C |
U min |
1250 |
2.57E-07 |
128 |
| |
|
|
|
|
| 1C |
Th min |
100 |
|
|
| |
|
|
|
|
| 1C |
U max |
3300 |
6.78E-07 |
475 |
| |
|
|
|
|
| 1C |
Th max |
275 |
|
|
| |
|
|
|
|
Table B6: Range of possible Q/Q0
values for the zircons from 960 meters.
| Zircon |
Element |
Current conc., ppm |
Q0 in ncc STP/μg after 30 -50%
boundary loss effects |
Measured
He (Q) ncc STP/μg from Humphreys et al.
(2003a) |
Rough Estimates of Q/Q0 for
Individual Zircons |
| 1A |
U min |
240 |
41.3 |
8.6 |
0.21 |
| |
|
|
|
|
|
| 1A |
Th min |
800 |
|
|
|
| |
|
|
|
|
|
| 1A |
U max |
5300 |
809 |
8.6 |
0.011 |
| |
|
|
|
|
|
| 1A |
Th max |
2000 |
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| 1B |
U min |
465 |
51.7 |
8.6 |
0.17 |
| |
|
|
|
|
|
| 1B |
Th min |
220 |
|
|
|
| |
|
|
|
|
|
| 1B |
U max |
1130 |
182 |
8.6 |
0.047 |
| |
|
|
|
|
|
| 1B |
Th max |
750 |
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| 1C |
U min |
1250 |
128 |
8.6 |
0.067 |
| |
|
|
|
|
|
| 1C |
Th min |
100 |
|
|
|
| |
|
|
|
|
|
| 1C |
U max |
3300 |
475 |
8.6 |
0.018 |
| |
|
|
|
|
|
| 1C |
Th max |
275 |
|
|
|